Módulo 7 - Regressão com covariáveis categóricas

Aula - Regressão linear com covariáveis categóricas.

head(PlantGrowth)

##   weight group
## 1   4.17  ctrl
## 2   5.58  ctrl
## 3   5.18  ctrl
## 4   6.11  ctrl
## 5   4.50  ctrl
## 6   4.61  ctrl

PlantGrowth$group <- factor(PlantGrowth$group, levels = c('ctrl', 'trt1', 'trt2'))

Vamos analisar a produção de massa seca sob as três condições experimentais (controle e dois tratamentos).

Análise descritiva

boxplot(weight ~ group, data = PlantGrowth, xlab = 'Grupo', ylab = 'Horas extras',
        las = 1)

with(PlantGrowth, by(weight, group, summary))

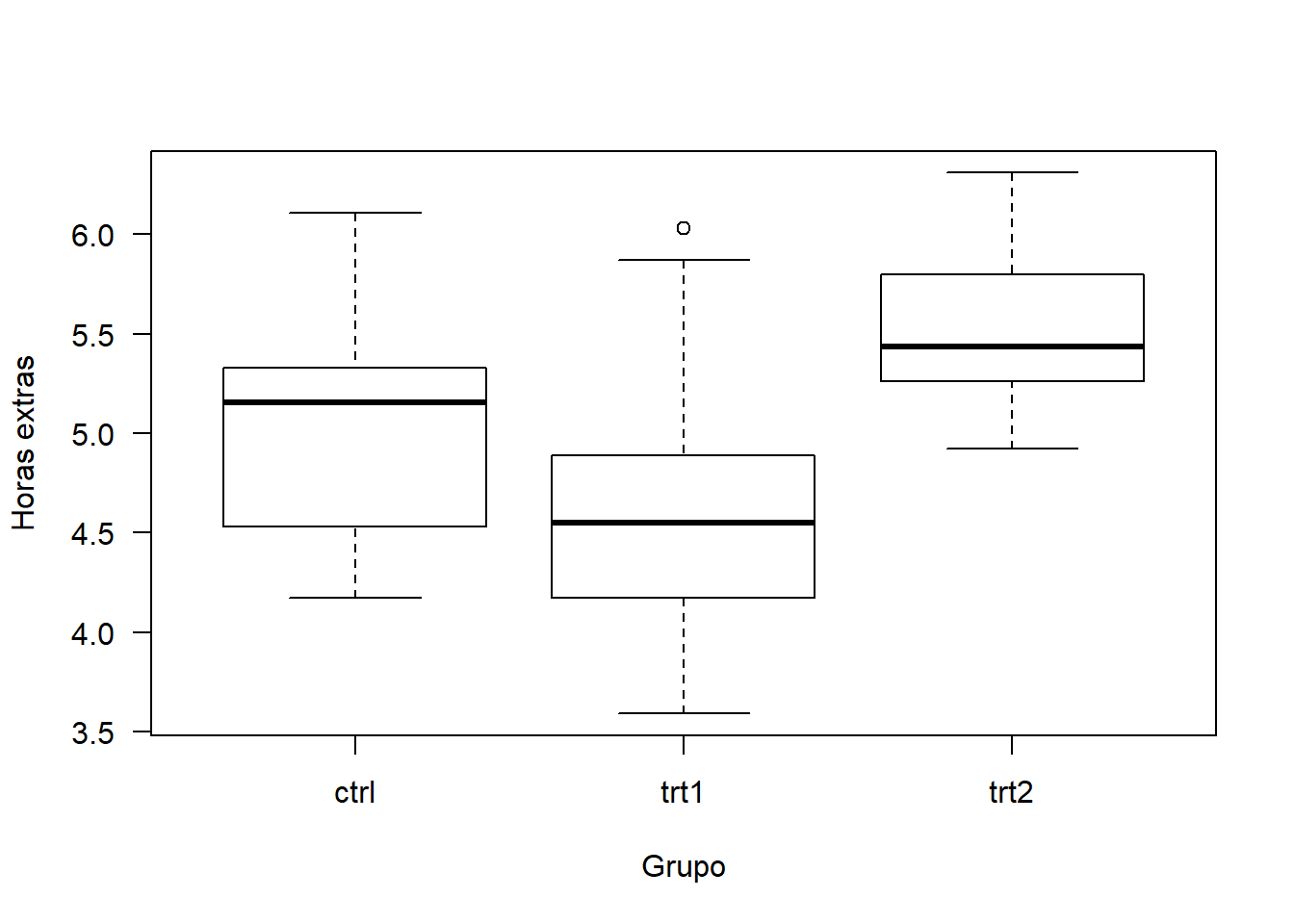
## group: ctrl
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   4.170   4.550   5.155   5.032   5.293   6.110 
## -------------------------------------------------------- 
## group: trt1
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   3.590   4.207   4.550   4.661   4.870   6.030 
## -------------------------------------------------------- 
## group: trt2
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   4.920   5.268   5.435   5.526   5.735   6.310

Considerar grupo controle e grupo com tratamento

Vamos considerar, num primeiro momento, apenas o grupo controle e o grupo com tratamento 1 (trt1)

PlantGrowth2 <- subset(PlantGrowth, group %in% c('ctrl', 'trt1'))

ajuste1 <- lm(weight ~ group, data = PlantGrowth2)
model.matrix(ajuste1)

##    (Intercept) grouptrt1
## 1            1         0
## 2            1         0
## 3            1         0
## 4            1         0
## 5            1         0
## 6            1         0
## 7            1         0
## 8            1         0
## 9            1         0
## 10           1         0
## 11           1         1
## 12           1         1
## 13           1         1
## 14           1         1
## 15           1         1
## 16           1         1
## 17           1         1
## 18           1         1
## 19           1         1
## 20           1         1
## attr(,"assign")
## [1] 0 1
## attr(,"contrasts")
## attr(,"contrasts")$group
## [1] "contr.treatment"

summary(ajuste1)

## 
## Call:
## lm(formula = weight ~ group, data = PlantGrowth2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.0710 -0.4938  0.0685  0.2462  1.3690 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   5.0320     0.2202  22.850 9.55e-15 ***
## grouptrt1    -0.3710     0.3114  -1.191    0.249    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6964 on 18 degrees of freedom
## Multiple R-squared:  0.07308,    Adjusted R-squared:  0.02158 
## F-statistic: 1.419 on 1 and 18 DF,  p-value: 0.249

Neste caso, o intercepto corresponde à estimativa do peso médio das plantas do grupo controle (5.03). A segunda estimativa apresentada corresponde à diferença no peso médio de plantas submwetidas ao tratamento 1 em relação a plantas do grupo controle (-0.37). A estimativa para o peso médio de plantas submetidas ao tratamento 1 é calculada por 5.03 - 0.37 = 4.66.

Vamos analisar os dados agora usando um teste t de comparação de médias, assumindo variâncias iguais nos dois grupos.

t.test(weight ~ group, data = PlantGrowth2, var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  weight by group
## t = 1.1913, df = 18, p-value = 0.249
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.2833003  1.0253003
## sample estimates:
## mean in group ctrl mean in group trt1 
##              5.032              4.661

Observe que o resultado do teste, bem como as estimativas apresentadas, são rigorosamente iguais às produzidas pelo modelo de regressão linear.

Três grupos

Vamos continuar a análise considerando os três grupos.

ajuste2 <- lm(weight ~ group, data = PlantGrowth)
model.matrix(ajuste2)

##    (Intercept) grouptrt1 grouptrt2
## 1            1         0         0
## 2            1         0         0
## 3            1         0         0
## 4            1         0         0
## 5            1         0         0
## 6            1         0         0
## 7            1         0         0
## 8            1         0         0
## 9            1         0         0
## 10           1         0         0
## 11           1         1         0
## 12           1         1         0
## 13           1         1         0
## 14           1         1         0
## 15           1         1         0
## 16           1         1         0
## 17           1         1         0
## 18           1         1         0
## 19           1         1         0
## 20           1         1         0
## 21           1         0         1
## 22           1         0         1
## 23           1         0         1
## 24           1         0         1
## 25           1         0         1
## 26           1         0         1
## 27           1         0         1
## 28           1         0         1
## 29           1         0         1
## 30           1         0         1
## attr(,"assign")
## [1] 0 1 1
## attr(,"contrasts")
## attr(,"contrasts")$group
## [1] "contr.treatment"

summary(ajuste2)

## 
## Call:
## lm(formula = weight ~ group, data = PlantGrowth)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.0710 -0.4180 -0.0060  0.2627  1.3690 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   5.0320     0.1971  25.527   <2e-16 ***
## grouptrt1    -0.3710     0.2788  -1.331   0.1944    
## grouptrt2     0.4940     0.2788   1.772   0.0877 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6234 on 27 degrees of freedom
## Multiple R-squared:  0.2641, Adjusted R-squared:  0.2096 
## F-statistic: 4.846 on 2 and 27 DF,  p-value: 0.01591

O intercepto novamente corresponde à estimativa do peso médio de plantas em condições semelhantes às do grupo controle. As demais estimativas correspondem às diferenças nas médias para cada grupo tratado em relação ao grupo controle.

Os resultados não apontam diferença significativa de peso, ao nível de 5%, para plantas submetidas ao tratamento 1 (p = 0.1944) e ao tratamento 2 (p = 0.0877) em relação ao grupo controle.

Vamos usar o teste F da análise de variância para avaliar a diferença entre os grupos.

anova(ajuste2)

## Analysis of Variance Table
## 
## Response: weight
##           Df  Sum Sq Mean Sq F value  Pr(>F)  
## group      2  3.7663  1.8832  4.8461 0.01591 *
## Residuals 27 10.4921  0.3886                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

O teste F indica diferença significativa, ao nível de significância de 5%, para as médias dos três grupos.

Mas o que dizer sobre a diferença dos efeitos dos tratamentos 1 e 2?

Podemos redefinir a categoria de referência da variável grupo:

PlantGrowth$group <- relevel(PlantGrowth$group, ref = 'trt2')

ajuste3 <- lm(weight ~ group, data = PlantGrowth)
model.matrix(ajuste3)

##    (Intercept) groupctrl grouptrt1
## 1            1         1         0
## 2            1         1         0
## 3            1         1         0
## 4            1         1         0
## 5            1         1         0
## 6            1         1         0
## 7            1         1         0
## 8            1         1         0
## 9            1         1         0
## 10           1         1         0
## 11           1         0         1
## 12           1         0         1
## 13           1         0         1
## 14           1         0         1
## 15           1         0         1
## 16           1         0         1
## 17           1         0         1
## 18           1         0         1
## 19           1         0         1
## 20           1         0         1
## 21           1         0         0
## 22           1         0         0
## 23           1         0         0
## 24           1         0         0
## 25           1         0         0
## 26           1         0         0
## 27           1         0         0
## 28           1         0         0
## 29           1         0         0
## 30           1         0         0
## attr(,"assign")
## [1] 0 1 1
## attr(,"contrasts")
## attr(,"contrasts")$group
## [1] "contr.treatment"

summary(ajuste3)

## 
## Call:
## lm(formula = weight ~ group, data = PlantGrowth)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.0710 -0.4180 -0.0060  0.2627  1.3690 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   5.5260     0.1971  28.032  < 2e-16 ***
## groupctrl    -0.4940     0.2788  -1.772  0.08768 .  
## grouptrt1    -0.8650     0.2788  -3.103  0.00446 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6234 on 27 degrees of freedom
## Multiple R-squared:  0.2641, Adjusted R-squared:  0.2096 
## F-statistic: 4.846 on 2 and 27 DF,  p-value: 0.01591

Há diferença significativa no peso médio de plantas sob os tratamentos 1 e 2. Estima-se, em média, 0.8650 a menos de peso sob tratamento 1 em relação ao tratamento 2.

Ao invés de redefinir o intercepto, vamos usar a função glht do pacote multcomp para estimar a diferença entre os dois tratamentos.

require(multcomp)

Vamos retomar o ajuste2, em que o grupo controle é a referência.

Estimativa da diferença dos pesos médios sob os tratamentos 1 e 2.

L <- rbind('Trat 1 - Trat 2' = c(0, 1, -1)); L

##                 [,1] [,2] [,3]
## Trat 1 - Trat 2    0    1   -1

g2 <- glht(ajuste2, linfct = L); g2

## 
##   General Linear Hypotheses
## 
## Linear Hypotheses:
##                      Estimate
## Trat 1 - Trat 2 == 0   -0.865

summary(g2)

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Fit: lm(formula = weight ~ group, data = PlantGrowth)
## 
## Linear Hypotheses:
##                      Estimate Std. Error t value Pr(>|t|)   
## Trat 1 - Trat 2 == 0  -0.8650     0.2788  -3.103  0.00446 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

confint(g2)

## 
##   Simultaneous Confidence Intervals
## 
## Fit: lm(formula = weight ~ group, data = PlantGrowth)
## 
## Quantile = 2.0518
## 95% family-wise confidence level
##  
## 
## Linear Hypotheses:
##                      Estimate lwr     upr    
## Trat 1 - Trat 2 == 0 -0.8650  -1.4370 -0.2930

E se quisermos as estimativas dos pesos médios para cada grupo? Para o grupo controle a estimativa é simplesmente o intercepto do modelo ajustado (beta0), e o resultado está no summary. Para o tratamento 1 devemos estimar beta0 + beta1 e para o tratamento 2 beta0 + beta2:

L <- rbind('Trat 1' = c(1, 1, 0),
           'Trat 2' = c(1, 0, 1)); L

##        [,1] [,2] [,3]
## Trat 1    1    1    0
## Trat 2    1    0    1

g2 <- glht(ajuste2, linfct = L); g2

## 
##   General Linear Hypotheses
## 
## Linear Hypotheses:
##             Estimate
## Trat 1 == 0    4.661
## Trat 2 == 0    5.526

estimativas pontuais para cada grupo.

summary(g2)

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Fit: lm(formula = weight ~ group, data = PlantGrowth)
## 
## Linear Hypotheses:
##             Estimate Std. Error t value Pr(>|t|)    
## Trat 1 == 0   4.6610     0.1971   23.64   <1e-10 ***
## Trat 2 == 0   5.5260     0.1971   28.03   <1e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

confint(g2)

## 
##   Simultaneous Confidence Intervals
## 
## Fit: lm(formula = weight ~ group, data = PlantGrowth)
## 
## Quantile = 2.3635
## 95% family-wise confidence level
##  
## 
## Linear Hypotheses:
##             Estimate lwr    upr   
## Trat 1 == 0 4.6610   4.1951 5.1269
## Trat 2 == 0 5.5260   5.0601 5.9919

Intervalos de confiança.

Sem intercepto

Agora vamos ajustar o modelo sem o intercepto.

contrasts(PlantGrowth$group) Padrão do R, contrastes de tratamentos, primeiro nível como referência.

Remoção do intercepto:

ajuste4 <- lm(weight ~ group - 1, data = PlantGrowth)
model.matrix(ajuste4)

##    grouptrt2 groupctrl grouptrt1
## 1          0         1         0
## 2          0         1         0
## 3          0         1         0
## 4          0         1         0
## 5          0         1         0
## 6          0         1         0
## 7          0         1         0
## 8          0         1         0
## 9          0         1         0
## 10         0         1         0
## 11         0         0         1
## 12         0         0         1
## 13         0         0         1
## 14         0         0         1
## 15         0         0         1
## 16         0         0         1
## 17         0         0         1
## 18         0         0         1
## 19         0         0         1
## 20         0         0         1
## 21         1         0         0
## 22         1         0         0
## 23         1         0         0
## 24         1         0         0
## 25         1         0         0
## 26         1         0         0
## 27         1         0         0
## 28         1         0         0
## 29         1         0         0
## 30         1         0         0
## attr(,"assign")
## [1] 1 1 1
## attr(,"contrasts")
## attr(,"contrasts")$group
## [1] "contr.treatment"

summary(ajuste4)

## 
## Call:
## lm(formula = weight ~ group - 1, data = PlantGrowth)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.0710 -0.4180 -0.0060  0.2627  1.3690 
## 
## Coefficients:
##           Estimate Std. Error t value Pr(>|t|)    
## grouptrt2   5.5260     0.1971   28.03   <2e-16 ***
## groupctrl   5.0320     0.1971   25.53   <2e-16 ***
## grouptrt1   4.6610     0.1971   23.64   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6234 on 27 degrees of freedom
## Multiple R-squared:  0.9867, Adjusted R-squared:  0.9852 
## F-statistic: 665.5 on 3 and 27 DF,  p-value: < 2.2e-16

confint(ajuste4)

##              2.5 %   97.5 %
## grouptrt2 5.121526 5.930474
## groupctrl 4.627526 5.436474
## grouptrt1 4.256526 5.065474

Cada estimativa agora corresponde à média sob uma das condições experimentais.

Outro exemplo

Regressão com covariáveis quantitativas e qualitativas. Exemplo 1 - Dados de reação enzimática com células tratadas ou não com Puromycin. Nesse caso a variável qualitativa tem dois níveis (tratado ou não tratado).

require(ggplot2)

help("Puromycin")

ggplot(aes(x = conc, y = rate, color = state), data = Puromycin) + geom_point() +
    theme_bw(base_size = 18)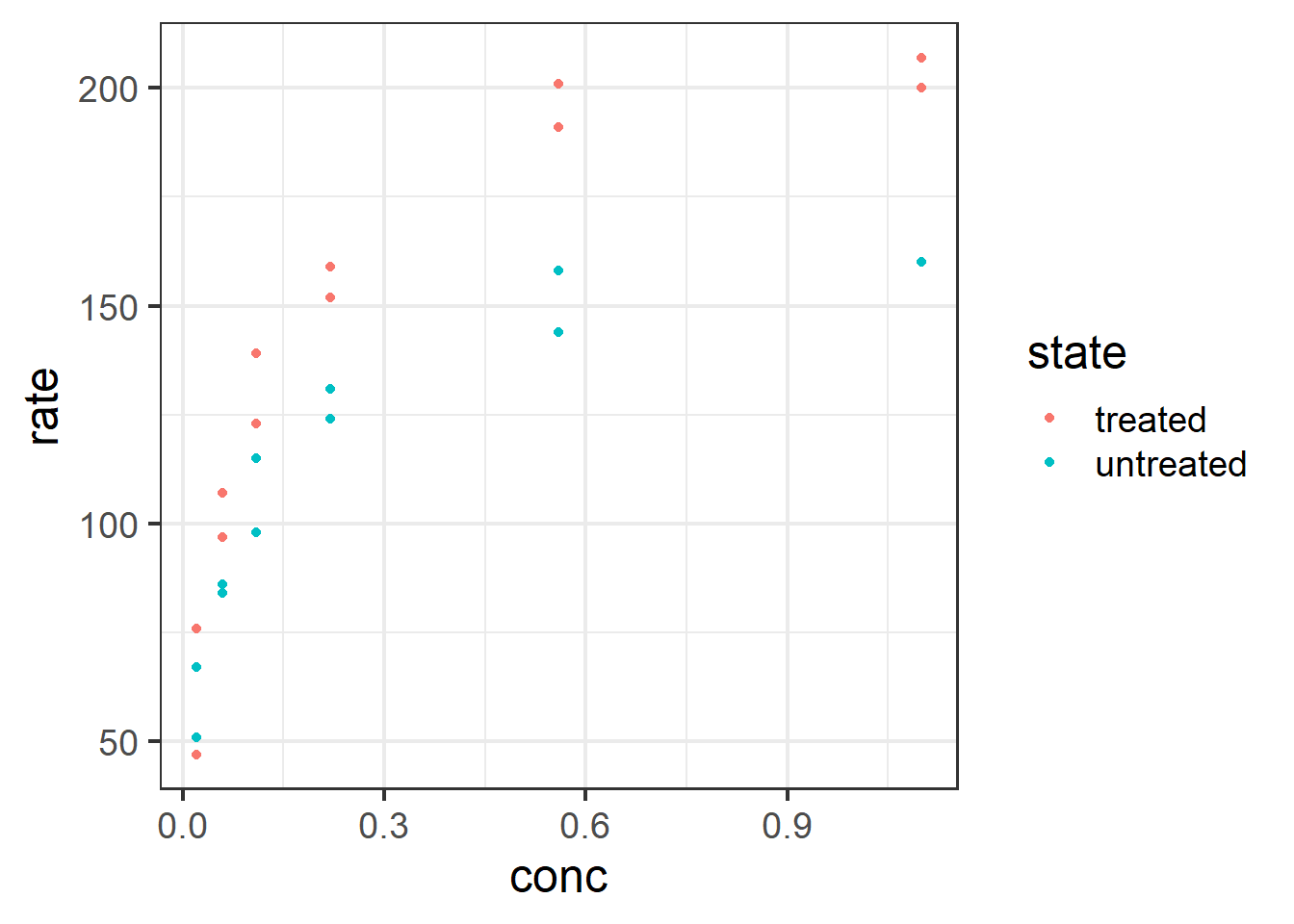

ggplot(aes(x = conc, y = rate), data = Puromycin) + geom_point() + 
    facet_grid(~state) + theme_bw(base_size = 18) +
    xlab('Concentração de substrato (ppm)') + 
    ylab('Taxa de reação (contagem/min^2)')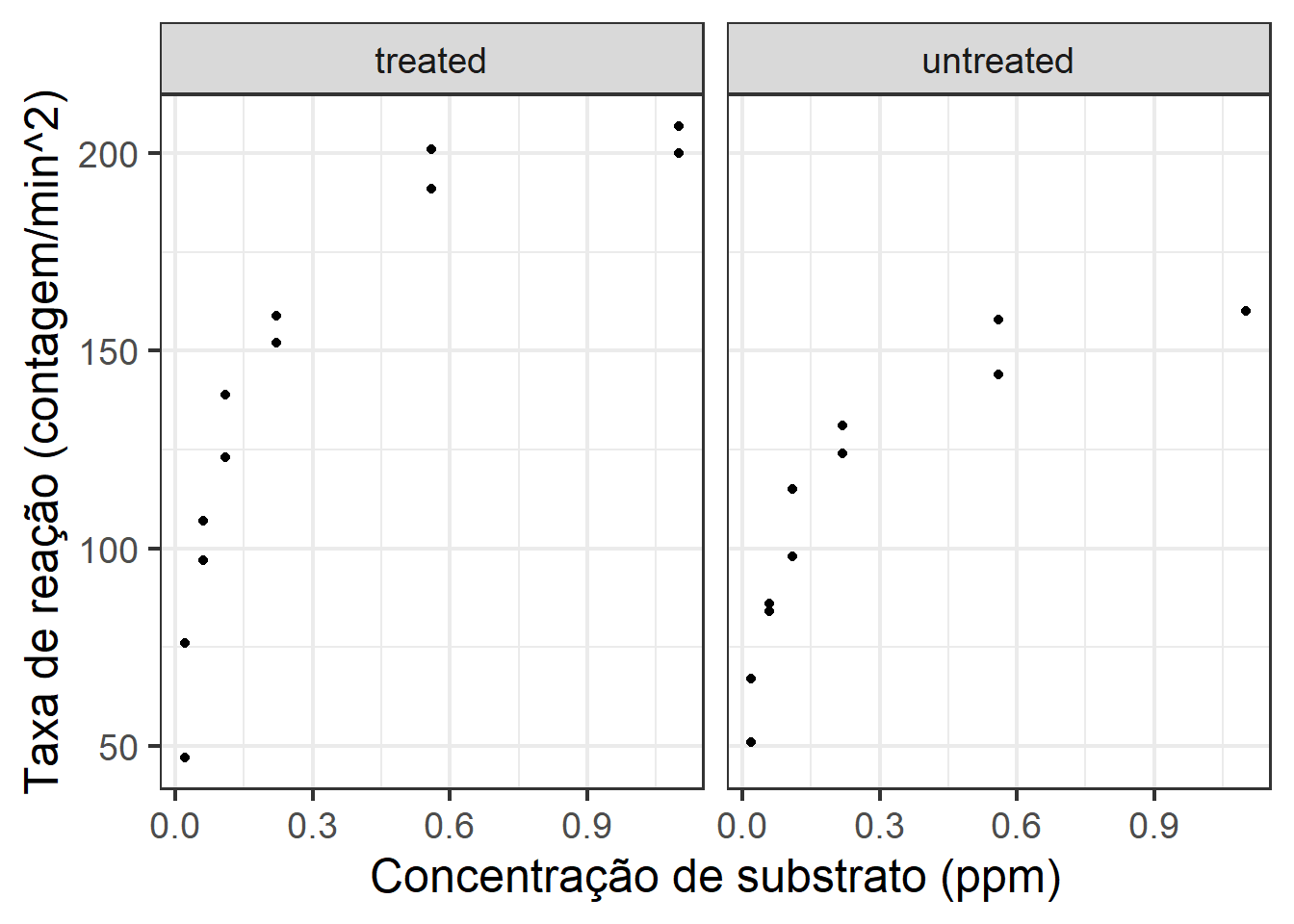

A relação entre a concentração de substrato e a taxa de reação é claramente não linear. Vamos prosseguir a análise considerando transformação logarítmica para a concentração.

Ajuste 1

Vamos ajustar quatro modelos, em ordem crescente de complexidade.

Ajuste 1 - Modelo nulo, sem efeito de concentração.

ajuste1 <- lm(rate ~ 1, data = Puromycin)

Ajuste 2

Ajuste2 - Modelo com efeito de concentração, sem efeito de tratamento.

ajuste2 <- lm(rate ~ I(log2(conc)), data = Puromycin)

Ajuste 3

Ajuste3 - Modelo com efeitos aditivos de concentração e tratamento (sem interação)

ajuste3 <- lm(rate ~ I(log2(conc)) + state, data = Puromycin)

Ajuste 4

Ajuste4 - Modelo com efeito multiplicativo de concentração e tratamento (com interação)

ajuste4 <- lm(rate ~ I(log2(conc)) * state, data = Puromycin)

anova(ajuste1, ajuste2, ajuste3, ajuste4)

## Analysis of Variance Table
## 
## Model 1: rate ~ 1
## Model 2: rate ~ I(log2(conc))
## Model 3: rate ~ I(log2(conc)) + state
## Model 4: rate ~ I(log2(conc)) * state
##   Res.Df   RSS Df Sum of Sq       F    Pr(>F)    
## 1     22 49665                                   
## 2     21  6210  1     43455 518.870 2.955e-15 ***
## 3     20  2587  1      3623  43.258 2.695e-06 ***
## 4     19  1591  1       996  11.892  0.002692 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

De acordo com os resultados:

A adição da (log)concentração ao modelo nulo tem efeito significativo (F=518.87, p < 0.001);

A adição do tratamento ao modelo ajustado pela (log) concentração tem efeito significativo (F=43.258, p < 0.001);

A adição da interação entre tratamento e (log) concentração ao modelo aditivo tem efeito significativo (F=11.892, p = 0.0026).

Dessa forma, o modelo selecionado para descrever a relação entre a concentração de substrato e taxa de reação requer tanto interceptos quanto slopes distintos para cada tratamento.

summary(ajuste4)

## 
## Call:
## lm(formula = rate ~ I(log2(conc)) * state, data = Puromycin)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -17.018  -6.381  -1.005   7.616  13.323 
## 
## Coefficients:
##                              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                   209.194      4.453  46.974  < 2e-16 ***
## I(log2(conc))                  25.723      1.364  18.858 9.25e-14 ***
## stateuntreated                -44.606      6.811  -6.549 2.85e-06 ***
## I(log2(conc)):stateuntreated   -7.020      2.036  -3.448  0.00269 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.151 on 19 degrees of freedom
## Multiple R-squared:  0.968,  Adjusted R-squared:  0.9629 
## F-statistic: 191.3 on 3 and 19 DF,  p-value: 2.267e-14

Gráficos de resíduos

par(mfrow = c(2,2))
plot(ajuste4)

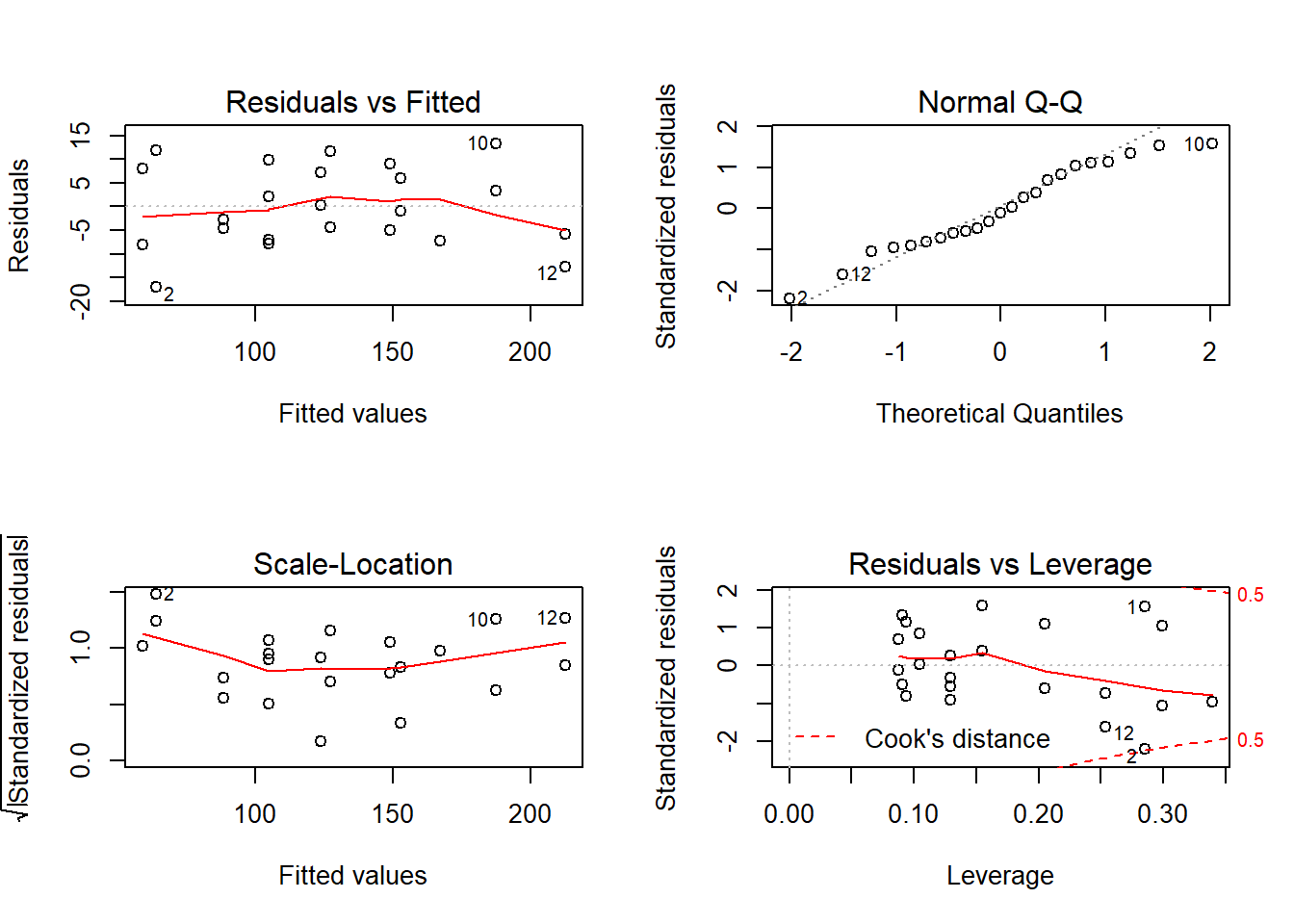
Acrescente seus comentários, produza resultados complementares.

Vamos plotar os ajustes. Para isso, primeiro vamos criar uma base para predição.

new_conc <- seq(min(Puromycin$conc), max(Puromycin$conc), length.out = 100)
trat <- c('treated', 'untreated')
new_data <- expand.grid(new_conc, trat)
names(new_data) <- c('conc', 'state')

Agora o gráfico.

ggplot(aes(x = conc, y = rate), data = Puromycin) + geom_point() + 
    facet_grid(~state) + theme_bw(base_size = 18) +
    xlab('Concentração de substrato (ppm)') + 
    ylab('Taxa de reação (contagem/min^2)') +
    geom_line(data = new_data, 
          aes(x = conc, y=predict(ajuste4, newdata=new_data)), 
          color='blue')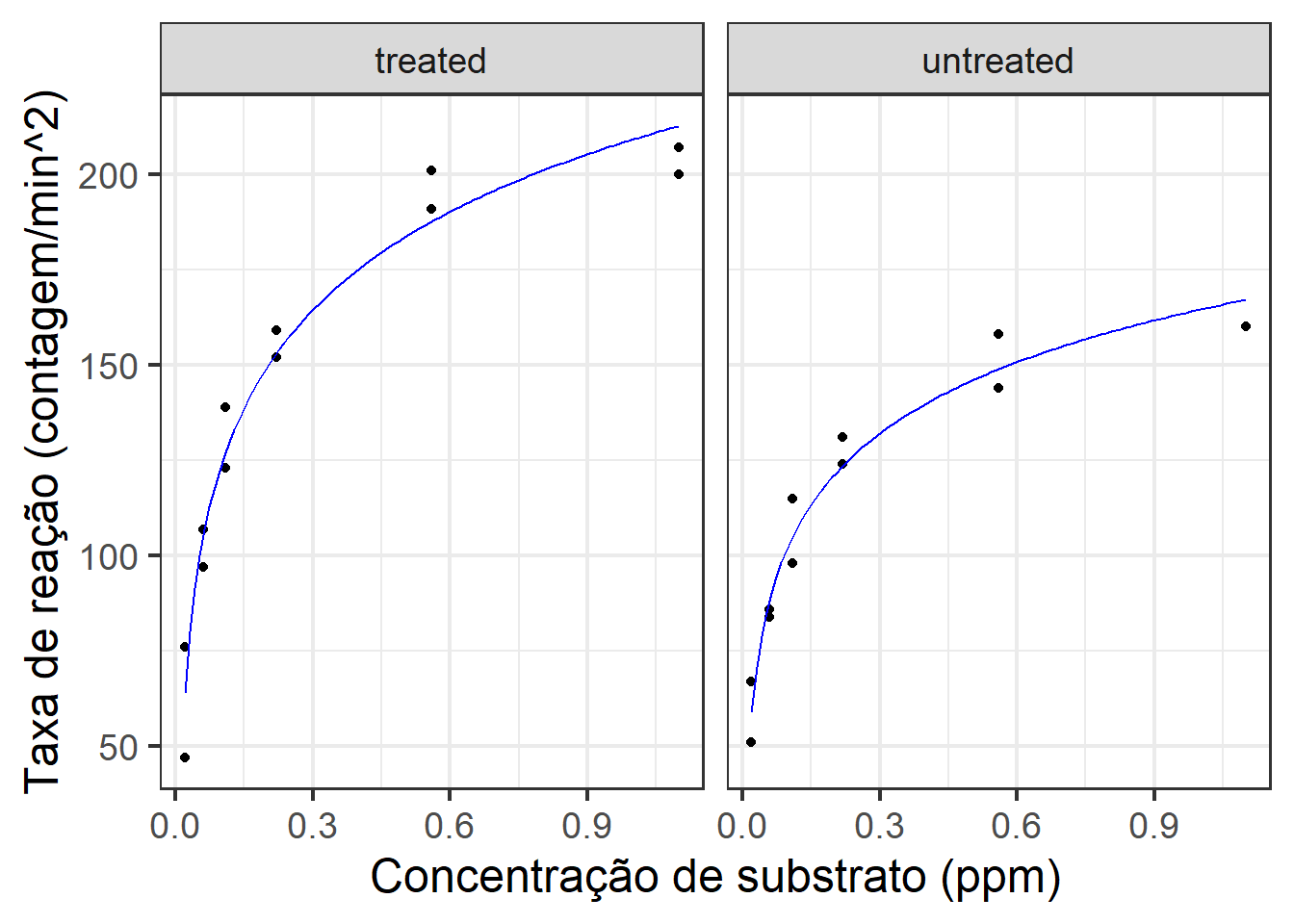

Outro exemplo

Regressão com covariáveis quantitativas e qualitativas. Exemplo 2 - Dados de logevidade de moscas machos submetidas a diferentes condições experimentais. Consulte a documentação.

require(faraway)
help("fruitfly")

ggplot(aes(x = thorax, y = longevity, color = activity), data = fruitfly) + geom_point() +
    theme_bw(base_size = 18)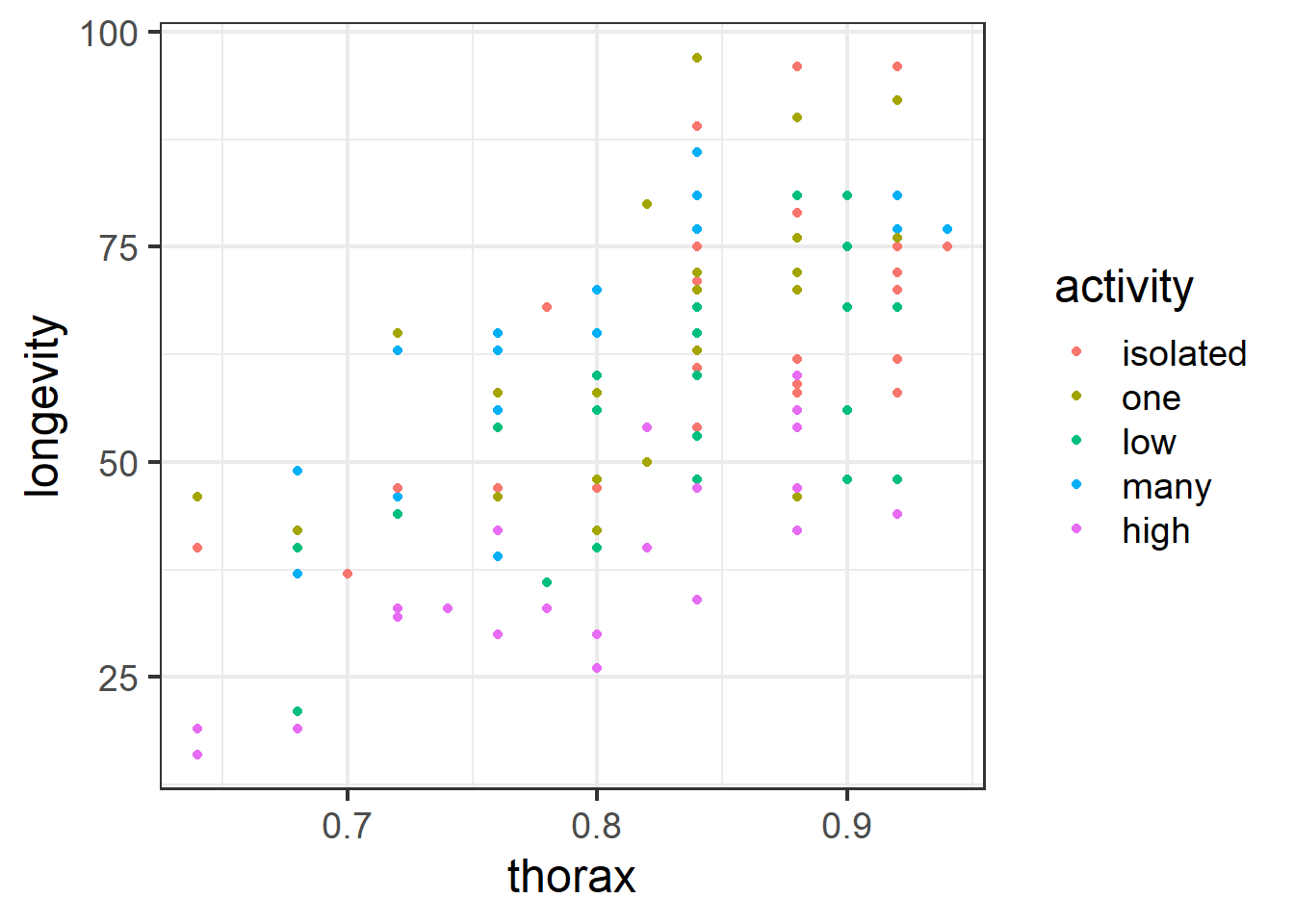

ggplot(aes(x = thorax, y = longevity), data = fruitfly) + geom_point() + 
    facet_grid(~activity) + theme_bw(base_size = 18) +
    xlab('Tamanho do torax') + 
    ylab('Tempo de vida (em dias)')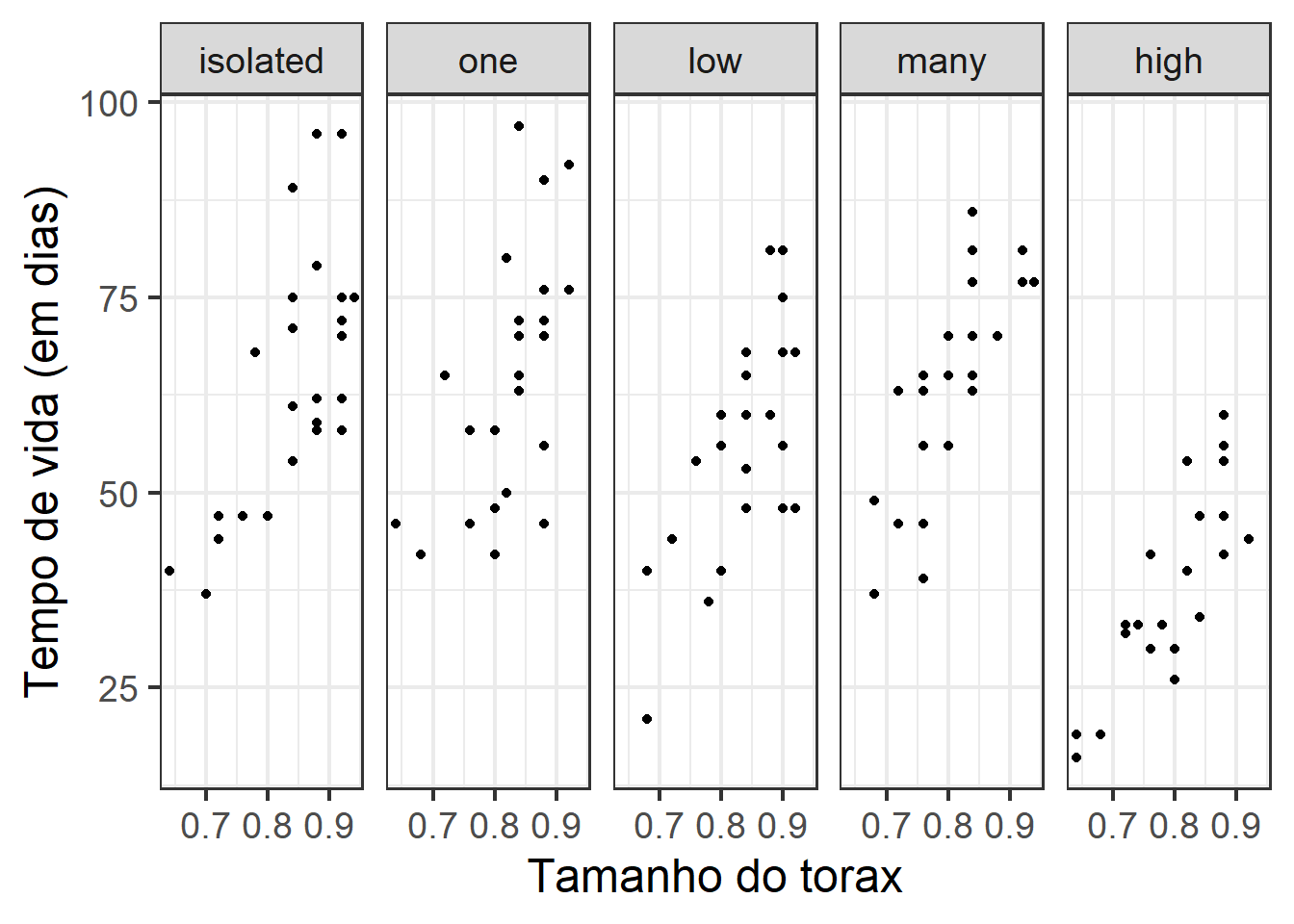

Vamos ajustar quatro modelos, em ordem crescente de complexidade.

Ajuste 1

Ajuste 1 - Modelo nulo, sem efeito de concentração.

ajuste1 <- lm(longevity ~ 1, data = fruitfly)

Ajuste 2

Ajuste2 - Modelo com efeito de concentração, sem efeito de tratamento.

ajuste2 <- lm(longevity ~ thorax, data = fruitfly)

Ajuste 3

Ajuste3 - Modelo com efeitos aditivos de concentração e tratamento (sem interação)

ajuste3 <- lm(longevity ~ thorax + activity, data = fruitfly)

Ajuste 4

Ajuste4 - Modelo com efeito multiplicativo de concentração e tratamento (com interação)

ajuste4 <- lm(longevity ~ thorax * activity, data = fruitfly)

anova(ajuste1, ajuste2, ajuste3, ajuste4)

## Analysis of Variance Table
## 
## Model 1: longevity ~ 1
## Model 2: longevity ~ thorax
## Model 3: longevity ~ thorax + activity
## Model 4: longevity ~ thorax * activity
##   Res.Df   RSS Df Sum of Sq       F    Pr(>F)    
## 1    123 37745                                   
## 2    122 22742  1   15003.3 130.733 < 2.2e-16 ***
## 3    118 13107  4    9634.6  20.988 5.503e-13 ***
## 4    114 13083  4      24.3   0.053    0.9947    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

De acordo com os resultados:

A adição do tamanho do torax ao modelo nulo tem efeito significativo (F=130.733, p < 0.001);

A adição do tratamento ao modelo ajustado pelo tamanho do torax tem efeito significativo (F=20.988, p < 0.001);

A adição da interação entre tamanho do torax e tratamento ao modelo aditivo não tem efeito significativo (F=0.053, p = 0.9947).

Dessa forma, o modelo selecionado para descrever a relação entre a concentração de substrato e taxa de reação requer um intercepto para cada tratamento, mas um único slope.

summary(ajuste3)

## 
## Call:
## lm(formula = longevity ~ thorax + activity, data = fruitfly)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -26.108  -7.014  -1.101   6.234  30.265 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -48.749     10.850  -4.493 1.65e-05 ***
## thorax        134.341     12.731  10.552  < 2e-16 ***
## activityone     2.637      2.984   0.884   0.3786    
## activitylow    -7.015      2.981  -2.353   0.0203 *  
## activitymany    4.139      3.027   1.367   0.1741    
## activityhigh  -20.004      3.016  -6.632 1.05e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.54 on 118 degrees of freedom
## Multiple R-squared:  0.6527, Adjusted R-squared:  0.638 
## F-statistic: 44.36 on 5 and 118 DF,  p-value: < 2.2e-16

Gráficos de resíduos

par(mfrow = c(2,2))
plot(ajuste3)

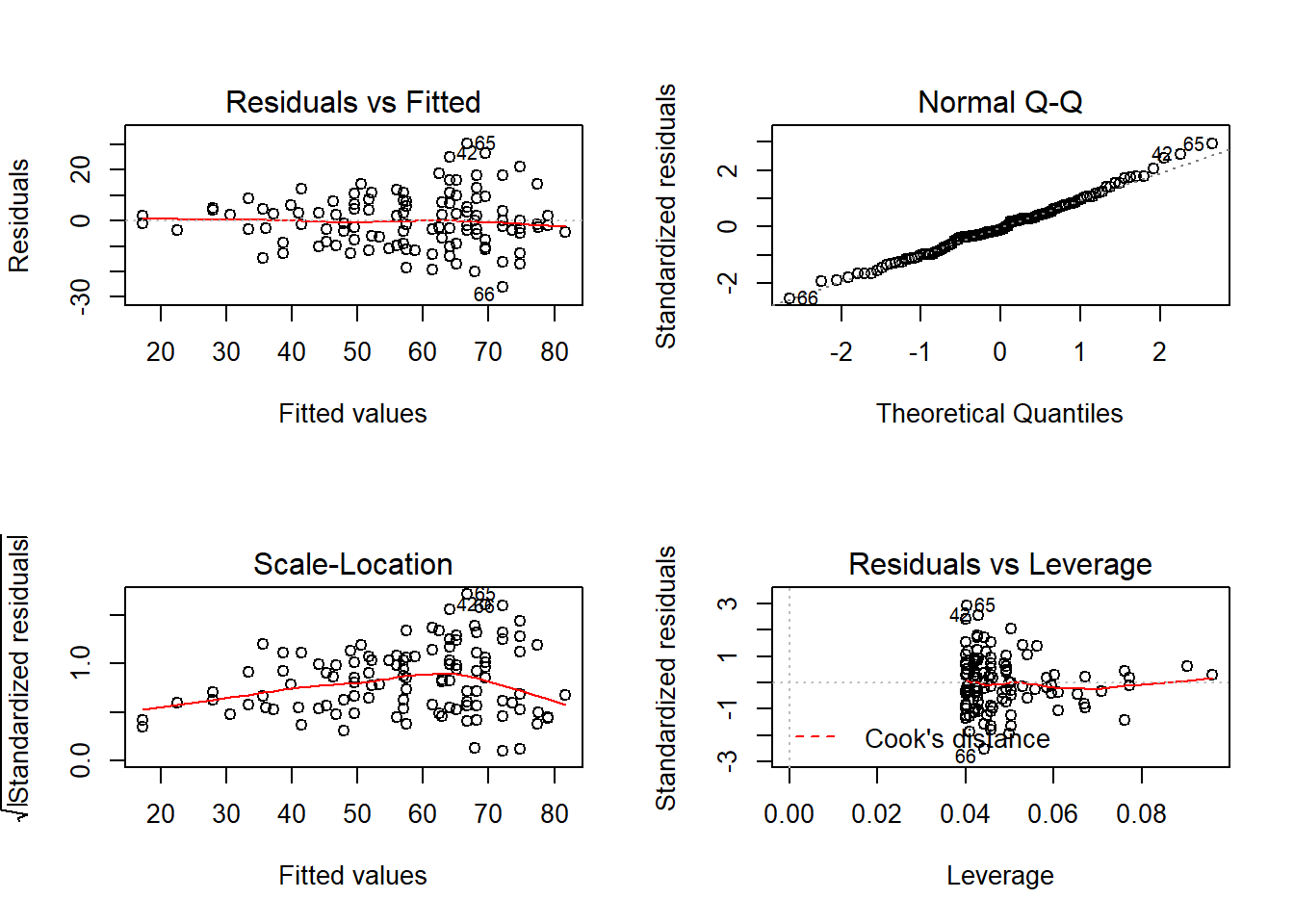
Os resíduos visivelmente não tem variância constante. Fica como tarefa encontrar uma transformação que contorne isso. Como o objetivo aqui é simplesmente obter as restas ajustadas (sem procupação quanto aos erros ou outras inferências, prosseguimos com o modelo original.)

Vamos plotar os ajustes. Para isso, primeiro vamos criar uma base para predição.

new_thorax <- seq(min(fruitfly$thorax), max(fruitfly$thorax), length.out = 100)
trat <- c('isolated', 'one', 'low', 'many', 'high')
new_data <- expand.grid(new_thorax, trat)
names(new_data) <- c('thorax', 'activity')

Agora o gráfico.

ggplot(aes(x = thorax, y = longevity), data = fruitfly) + geom_point() + 
    facet_grid(~activity) + theme_bw(base_size = 18) +
    xlab('Concentração de substrato (ppm)') + 
    ylab('Taxa de reação (contagem/min^2)') +
    geom_smooth(method='lm')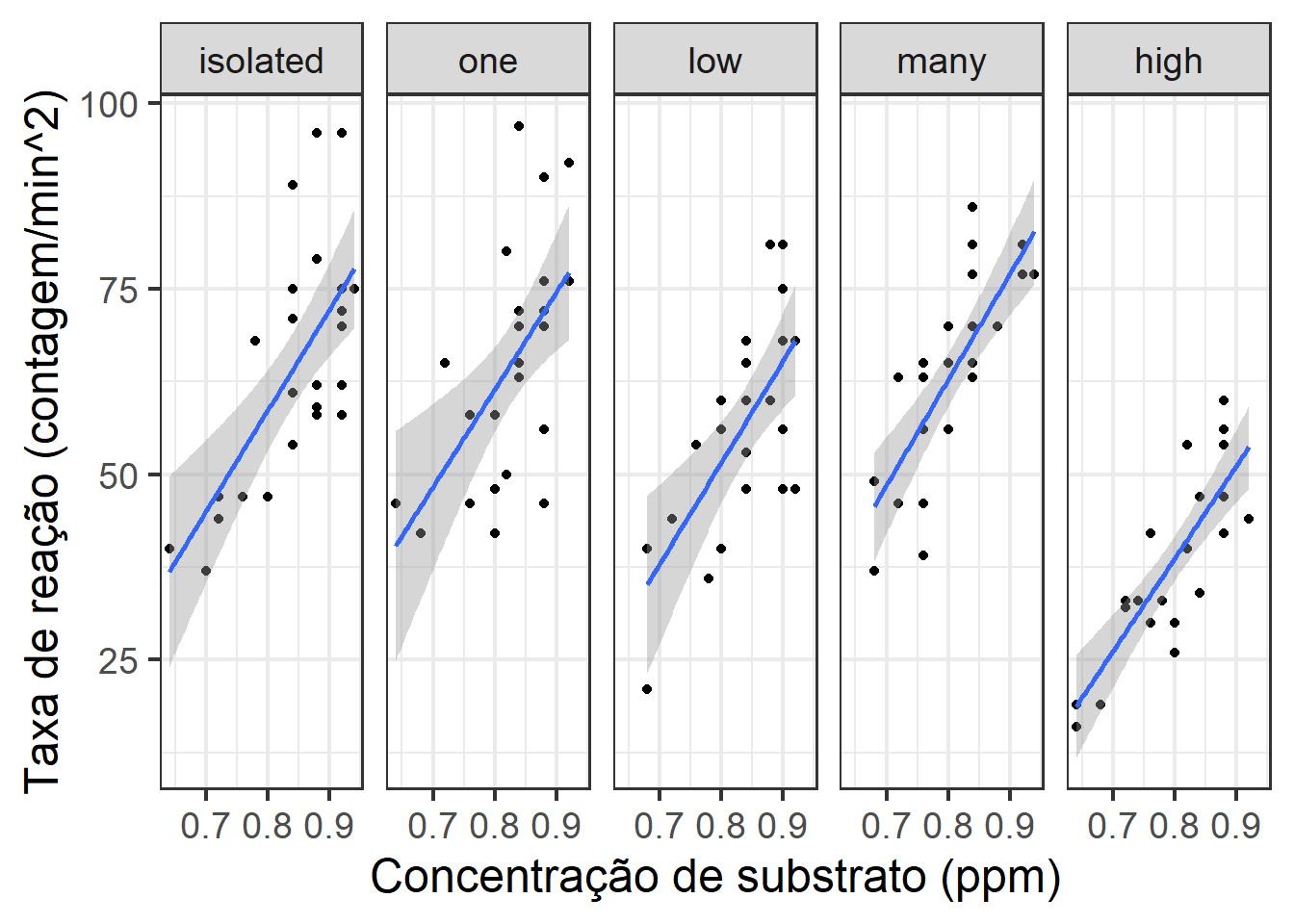

fruitfly$activity2 <- fruitfly$activity 
levels(fruitfly$activity2) <- c('iso or preg', 'iso or preg', 'virg1', 'iso or preg', 'virg2')
ajuste3_alt <- lm(longevity ~ thorax + activity2, data = fruitfly)
summary(ajuste3_alt)

## 
## Call:
## lm(formula = longevity ~ thorax + activity2, data = fruitfly)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -25.6102  -7.5189  -0.4157   6.3342  30.6952 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     -45.110     10.518  -4.289 3.65e-05 ***
## thorax          132.637     12.665  10.473  < 2e-16 ***
## activity2virg1   -9.226      2.443  -3.777 0.000248 ***
## activity2virg2  -22.279      2.458  -9.066 2.87e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.54 on 120 degrees of freedom
## Multiple R-squared:  0.6471, Adjusted R-squared:  0.6383 
## F-statistic: 73.34 on 3 and 120 DF,  p-value: < 2.2e-16

anova(ajuste3_alt, ajuste3)

## Analysis of Variance Table
## 
## Model 1: longevity ~ thorax + activity2
## Model 2: longevity ~ thorax + activity
##   Res.Df   RSS Df Sum of Sq      F Pr(>F)
## 1    120 13321                           
## 2    118 13107  2    213.89 0.9628 0.3848

Vamos testar agora se uma única reta de regressão é suficiente para explicar a relação entre longevidade e tamanho do torax para controle e para os dois grupos expostos a fêmeas grávidas.

fruitfly$activity2 <- fruitfly$activity 
levels(fruitfly$activity2) <- c('iso or preg', 'iso or preg', 'low', 'iso or preg', 'high')

O fator activity2 tem três níveis: ‘iso or preg’ para animais do grupo controle e submetidos a fêmeas grávidas; ‘low’ e ‘high’ para os outros dois grupos.

ajuste3_alt <- lm(longevity ~ thorax + activity2, data = fruitfly)

Modelo de regressão ajustado para o tratamento com três níveis.

Vamos comparar os ajustes dos modelos considerando o tratamento com cinco e com três níveis.

summary(ajuste3_alt)

## 
## Call:
## lm(formula = longevity ~ thorax + activity2, data = fruitfly)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -25.6102  -7.5189  -0.4157   6.3342  30.6952 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    -45.110     10.518  -4.289 3.65e-05 ***
## thorax         132.637     12.665  10.473  < 2e-16 ***
## activity2low    -9.226      2.443  -3.777 0.000248 ***
## activity2high  -22.279      2.458  -9.066 2.87e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.54 on 120 degrees of freedom
## Multiple R-squared:  0.6471, Adjusted R-squared:  0.6383 
## F-statistic: 73.34 on 3 and 120 DF,  p-value: < 2.2e-16

anova(ajuste3_alt, ajuste3)

## Analysis of Variance Table
## 
## Model 1: longevity ~ thorax + activity2
## Model 2: longevity ~ thorax + activity
##   Res.Df   RSS Df Sum of Sq      F Pr(>F)
## 1    120 13321                           
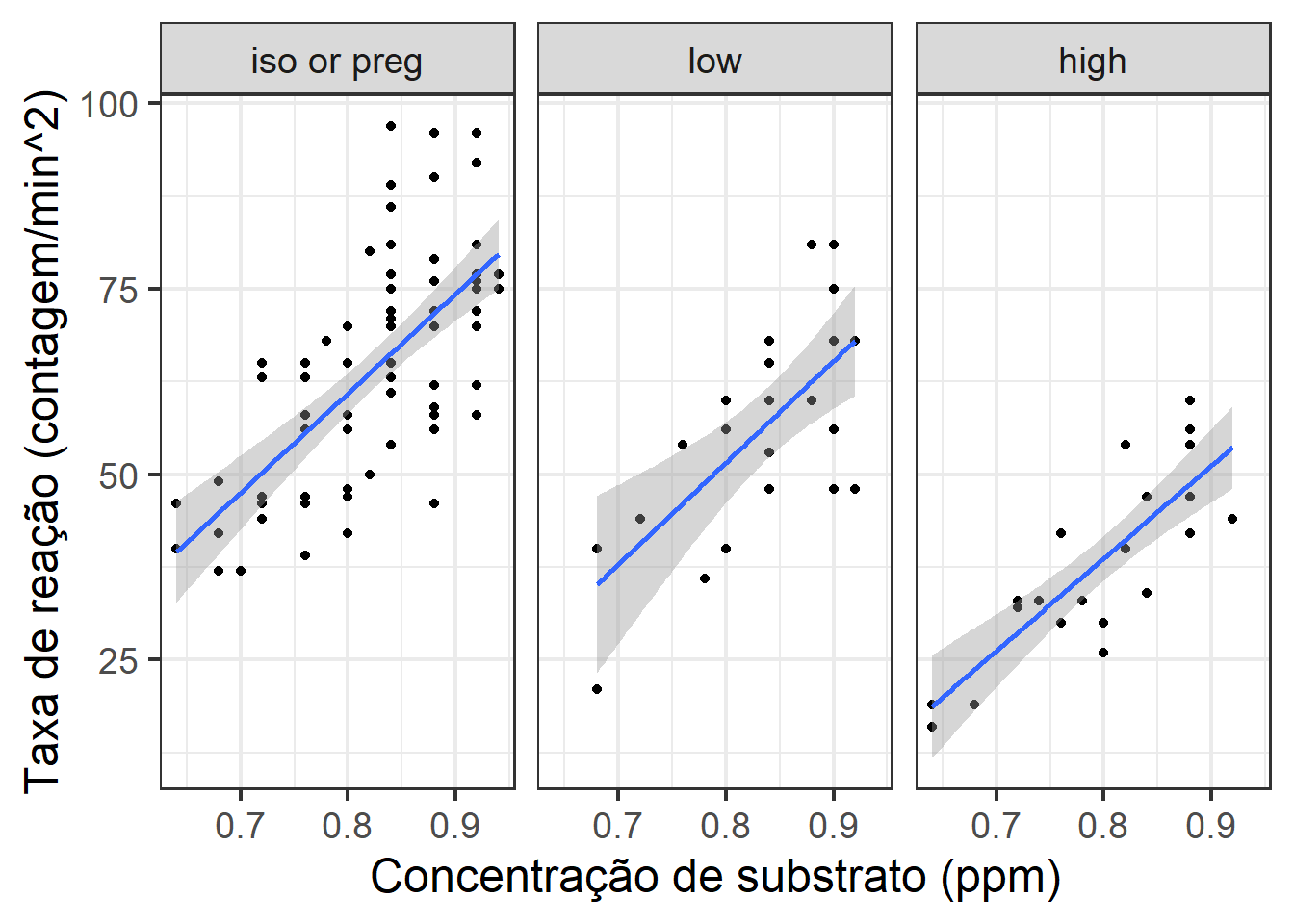
## 2    118 13107  2    213.89 0.9628 0.3848

Observe que o acréscimo na soma de quadrados resultante da redução de cinco para três níveis do tratamento é não significativa (p=0.3848). Assim, podemos considerar o modelo aditivo com uma única reta de regressão para os grupos ‘isolated’, ‘one’ e ‘many’.

Vamos plotar os resultados do ajuste, como feito anteriormente.

new_thorax <- seq(min(fruitfly$thorax), max(fruitfly$thorax), length.out = 100)
trat <- c('virg1', 'iso or preg', 'virg2')
new_data <- expand.grid(new_thorax, trat)
names(new_data) <- c('thorax', 'activity2')

ggplot(aes(x = thorax, y = longevity), data = fruitfly) + geom_point() + 
    facet_grid(~activity2) + theme_bw(base_size = 18) +
    xlab('Concentração de substrato (ppm)') + 
    ylab('Taxa de reação (contagem/min^2)') +
    geom_smooth(method='lm')