Diagnóstico do ajuste do modelo de regressão linear
Gian Lima
Matriz dos Scatterplots
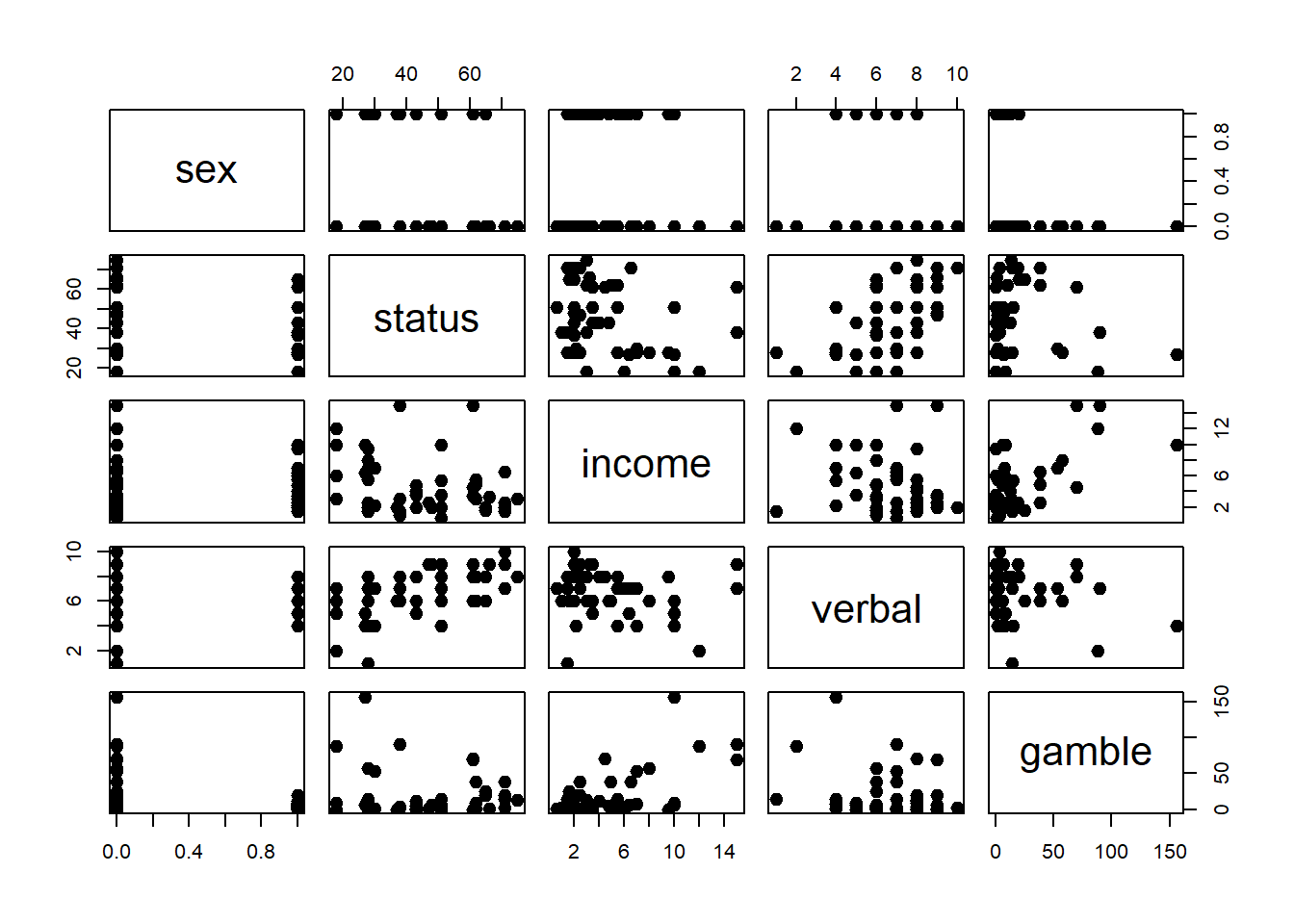
Modelo e ANOVA
##
## Call:
## lm(formula = gamble ~ ., data = teengamb)
##
## Residuals:
## Min 1Q Median 3Q Max
## -51.082 -11.320 -1.451 9.452 94.252
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.55565 17.19680 1.312 0.1968
## sex -22.11833 8.21111 -2.694 0.0101 *
## status 0.05223 0.28111 0.186 0.8535
## income 4.96198 1.02539 4.839 1.79e-05 ***
## verbal -2.95949 2.17215 -1.362 0.1803
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 22.69 on 42 degrees of freedom
## Multiple R-squared: 0.5267, Adjusted R-squared: 0.4816
## F-statistic: 11.69 on 4 and 42 DF, p-value: 1.815e-06Diagnóstico do ajuste


Tipos de resíduos: (5)


1. Resíduos ordinários
## 1 2 3 4 5
## 10.650743 9.371132 5.463030 -17.495749 29.5194692. Resíduos padronizados

## 1 2 3 4 5
## 0.4693954 0.4130009 0.2407645 -0.7710659 1.30097073. Resíduos studentizados

## 1 2 3 4 5
## 0.4893473 0.4374148 0.2487901 -0.8140147 1.40178884. Resíduos studentizados externamente

## 1 2 3 4 5
## 0.4848708 0.4331639 0.2459918 -0.8106860 1.41858275. Resíduos PRESS
## 1 2 3 4 5
## 11.575413 10.511798 5.833307 -19.499075 34.271941Análise de Resíduos


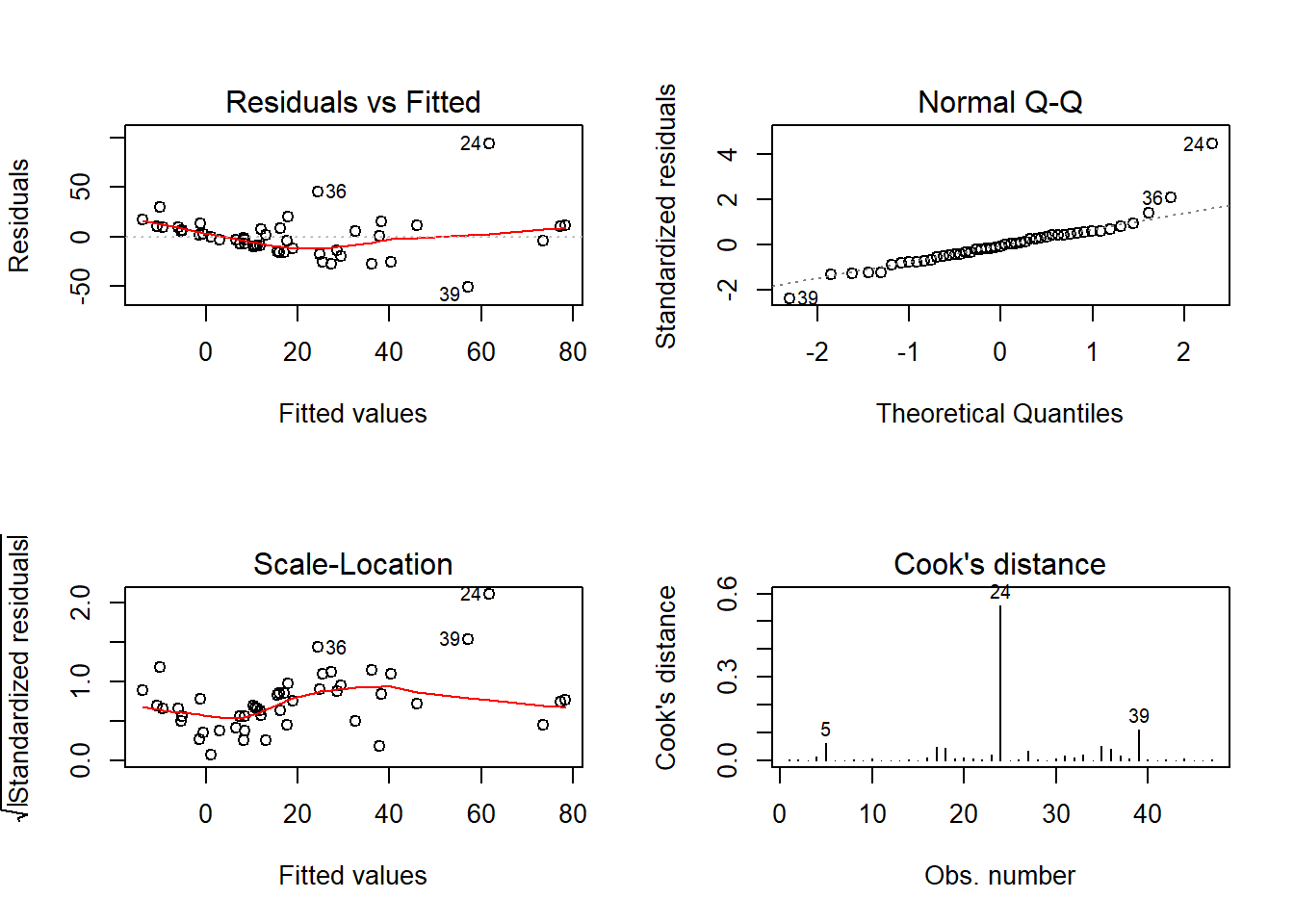
Gráfico de Resíduos vs Valores Ajustados
fit <- fitted(ajuste)
res <- rstudent(ajuste)
par(cex = 1.4, las = 1)
plot(fit, res, xlab = 'Valores ajustados', ylab = 'Resíduos studentizados', pch = 20)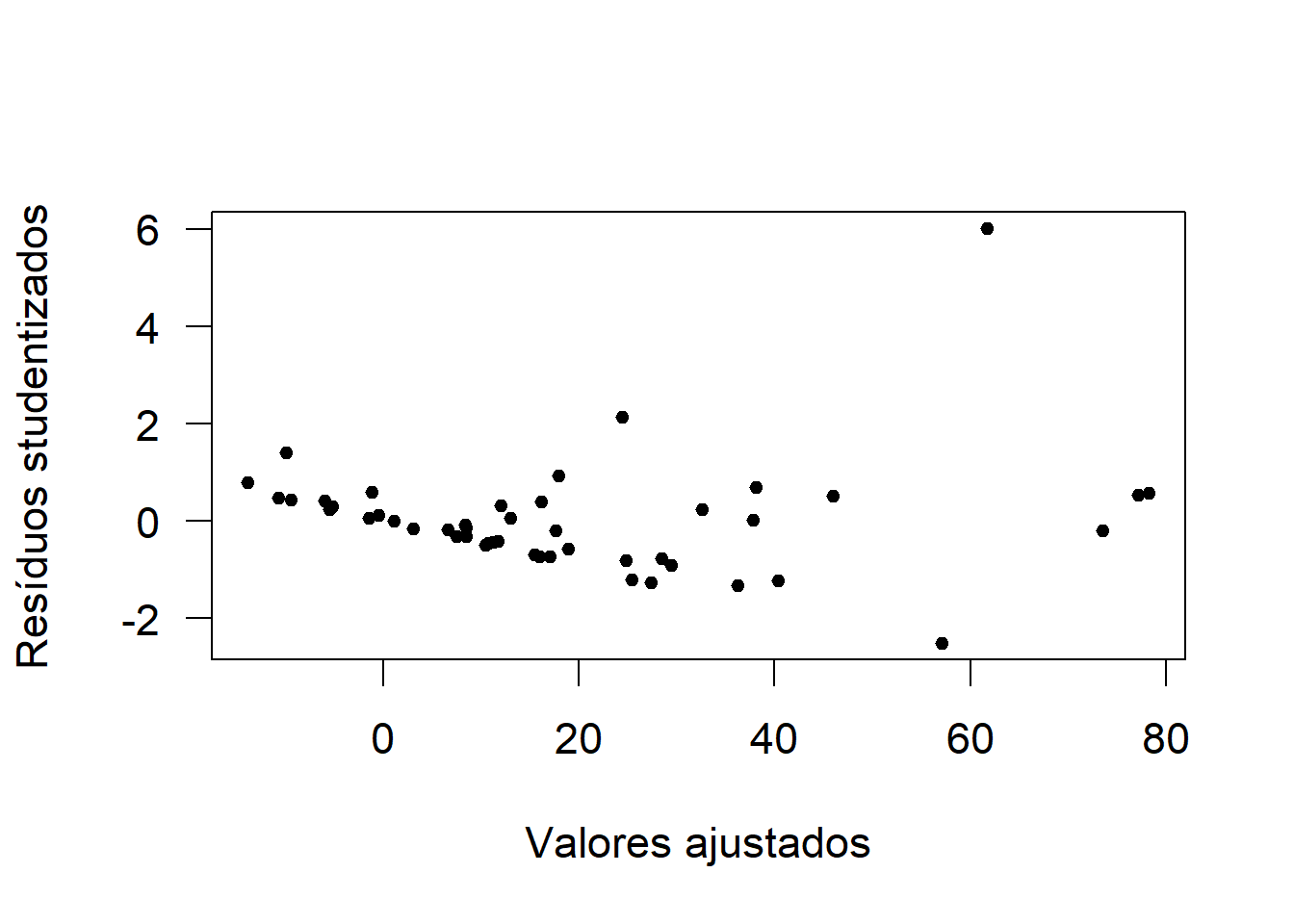
Fica bastante evidente que os resíduos não apresentam variância constante.
Testes de Hipótese


Teste de variância constante
\[H_0: \text{Resíduos têm variância constante}\]
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 24.29051, Df = 1, p = 8.2846e-07Temos evidência altamente significativa de variância não constante.
Teste de normalidade para os resíduos (Shapiro-Wilk)
\[H_0: \text{Os resíduos seguem distribuição normal }\]
##
## Shapiro-Wilk normality test
##
## data: rstudent(ajuste)
## W = 0.76398, p-value = 2.706e-07A hipótese de normalidade é rejeitada.
Gráfico quantil-quantil com envelope de confiança
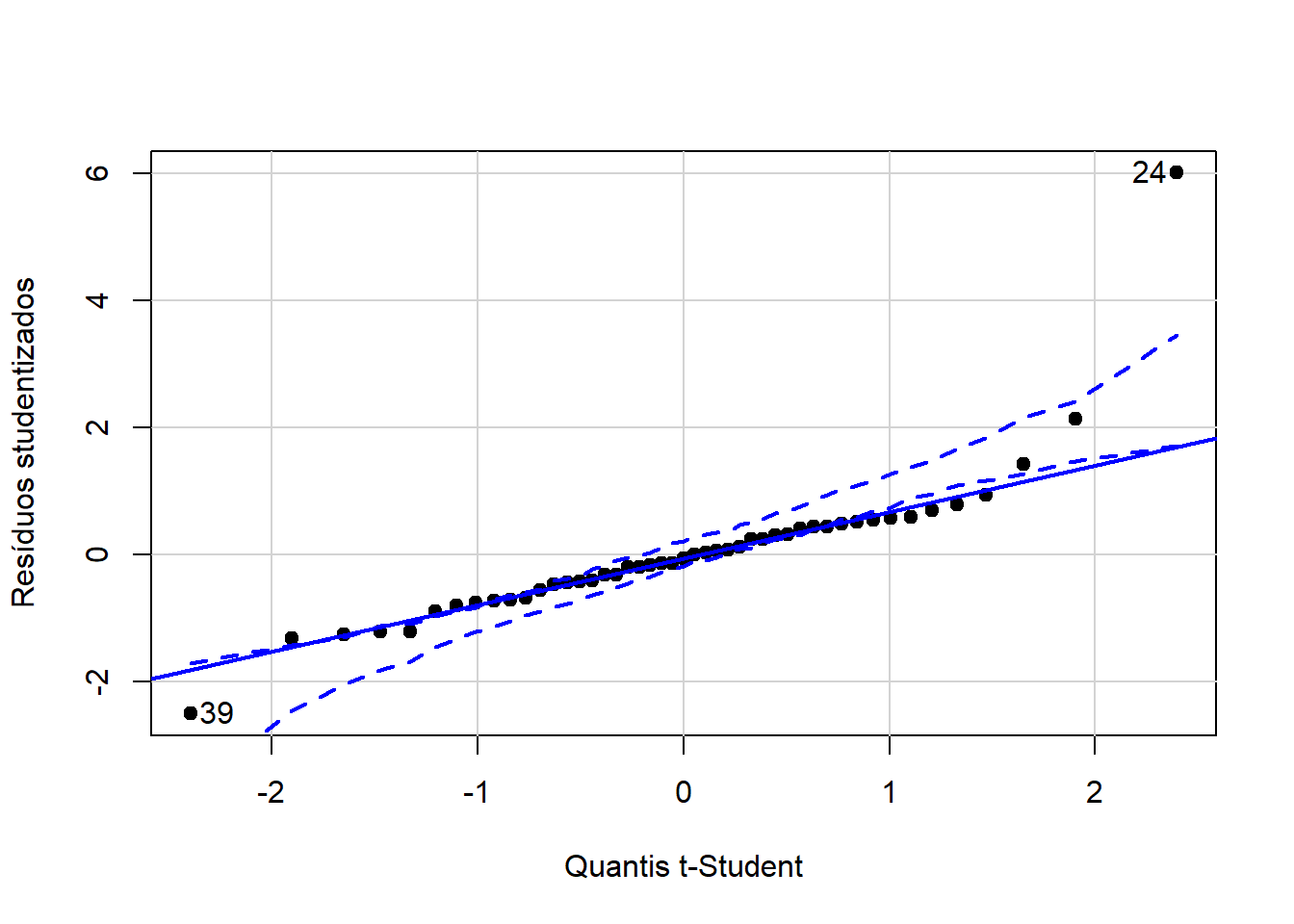
## [1] 24 39Os resíduos não apresentam boa aderência à distribuição t-Student de referência.
Resíduos vs variáveis incluídas no modelo
par(mfrow=c(2,2))
plot(teengamb$sex, res, xlab = 'Sexo', ylab = 'Resíduos studentizados', pch = 20)
plot(teengamb$status, res, xlab = 'Status', ylab = 'Resíduos studentizados', pch = 20)
plot(teengamb$income, res, xlab = 'Income', ylab = 'Resíduos studentizados', pch = 20)
plot(teengamb$verbal, res, xlab = 'Verbal', ylab = 'Resíduos studentizados', pch = 20)
lines(lowess(res ~ teengamb$verbal), lwd = 2, col = 'red')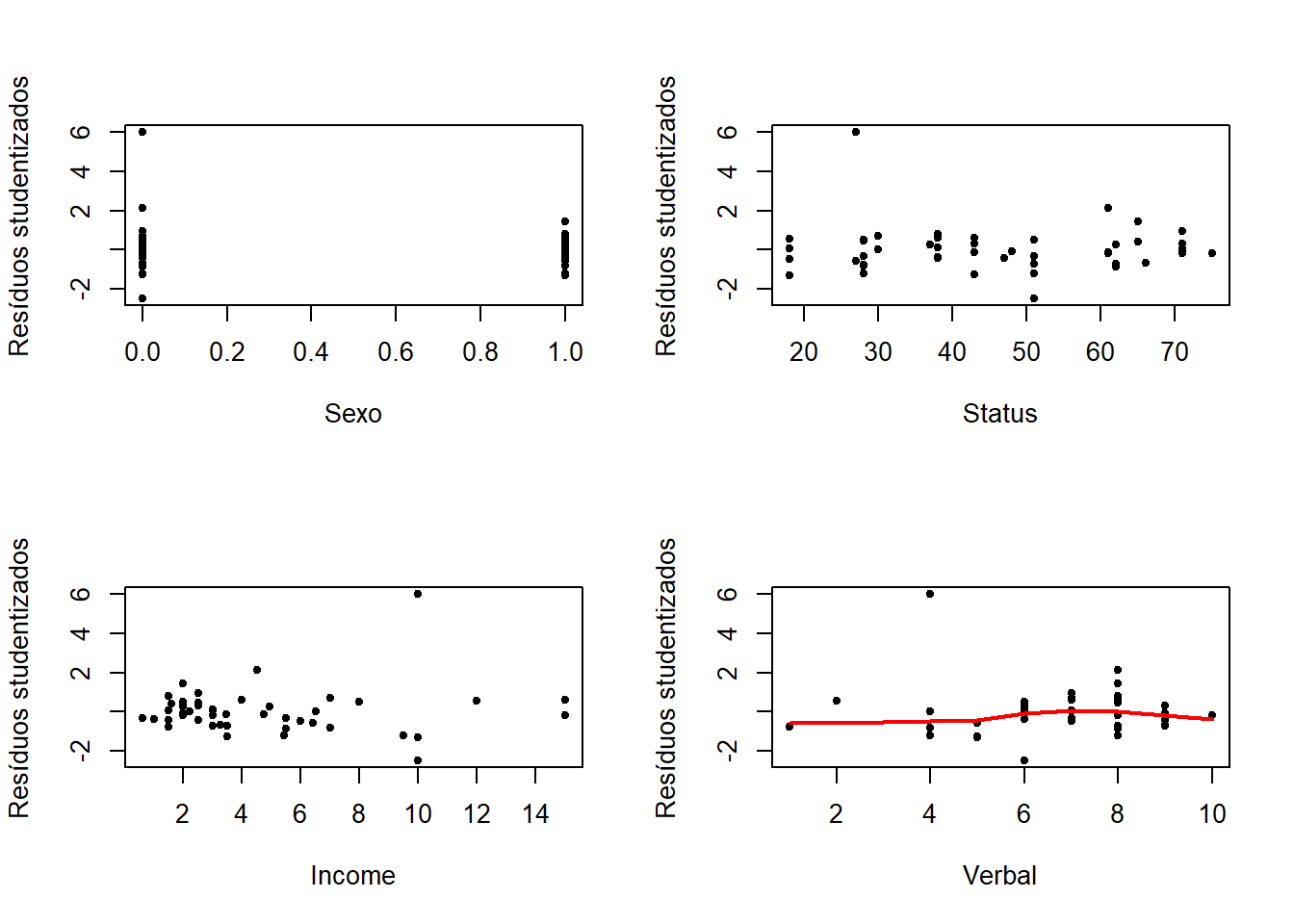
A variância dos resíduos não aparenta ser constante em relação às variáveis sexo e income.
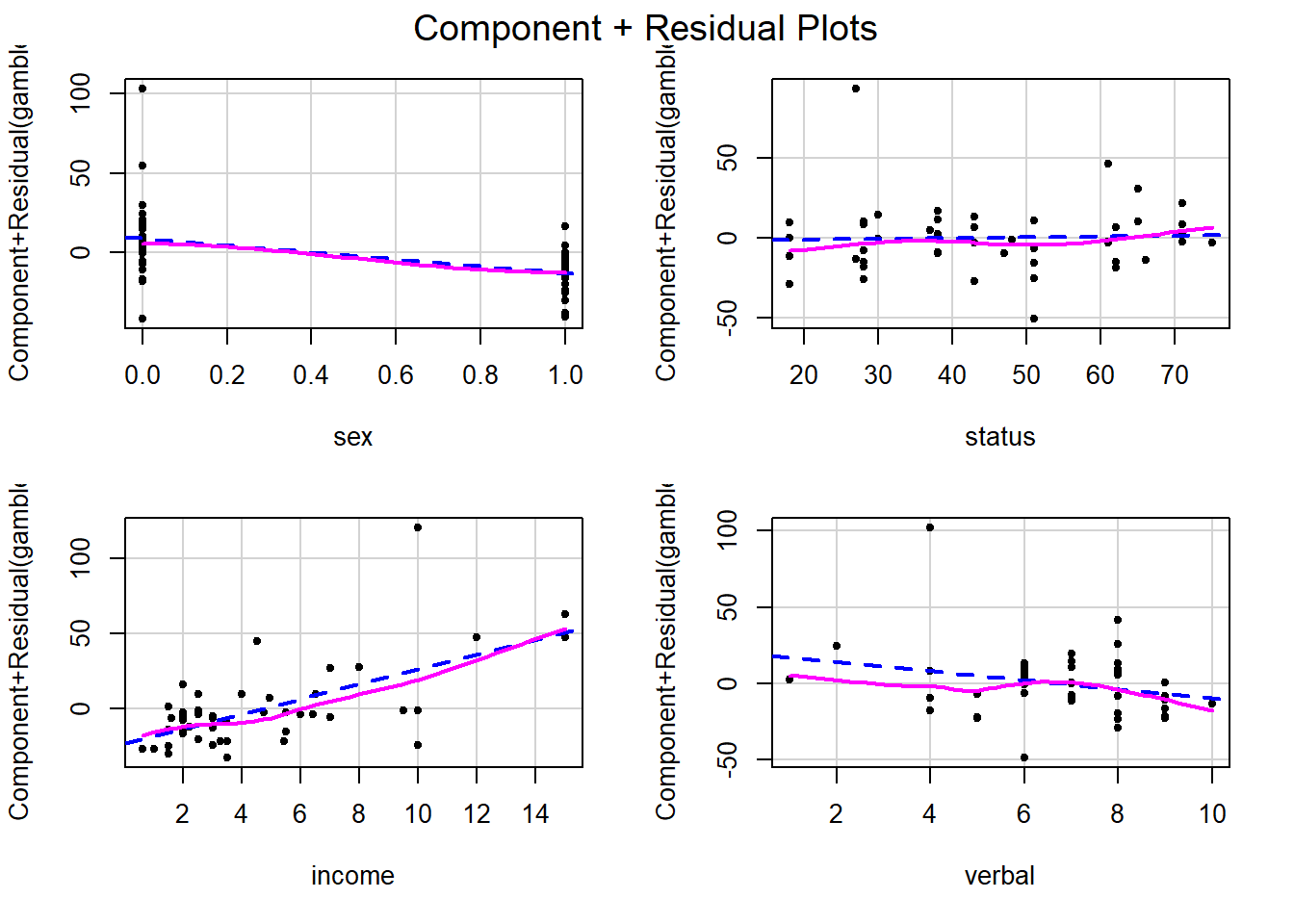
Gráficos de resíduos parciais
par(mfrow=c(2,2))
termplot(ajuste, partial.resid = TRUE, terms = 1, pch = 20, col.res = 'black')
termplot(ajuste, partial.resid = TRUE, terms = 2, pch = 20, col.res = 'black')
termplot(ajuste, partial.resid = TRUE, terms = 3, pch = 20, col.res = 'black')
termplot(ajuste, partial.resid = TRUE, terms = 4, pch = 20, col.res = 'black')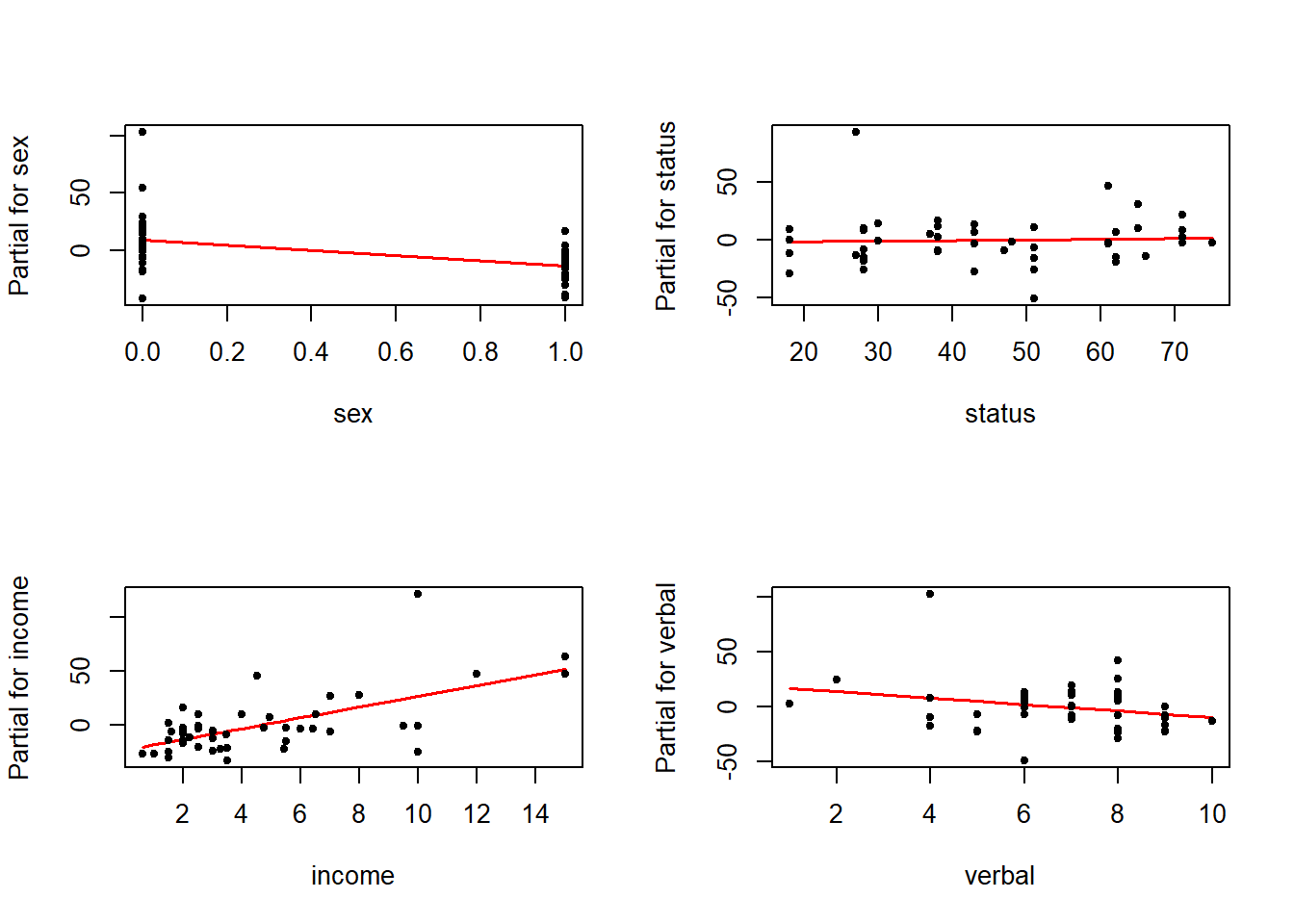
Os gráficos de resíduos parciais evidenciam a relação entre sexo e income (linear?) com a resposta (ajustado pelo efeito das demais variáveis).
Usando recursos de diagnóstico do pacote car
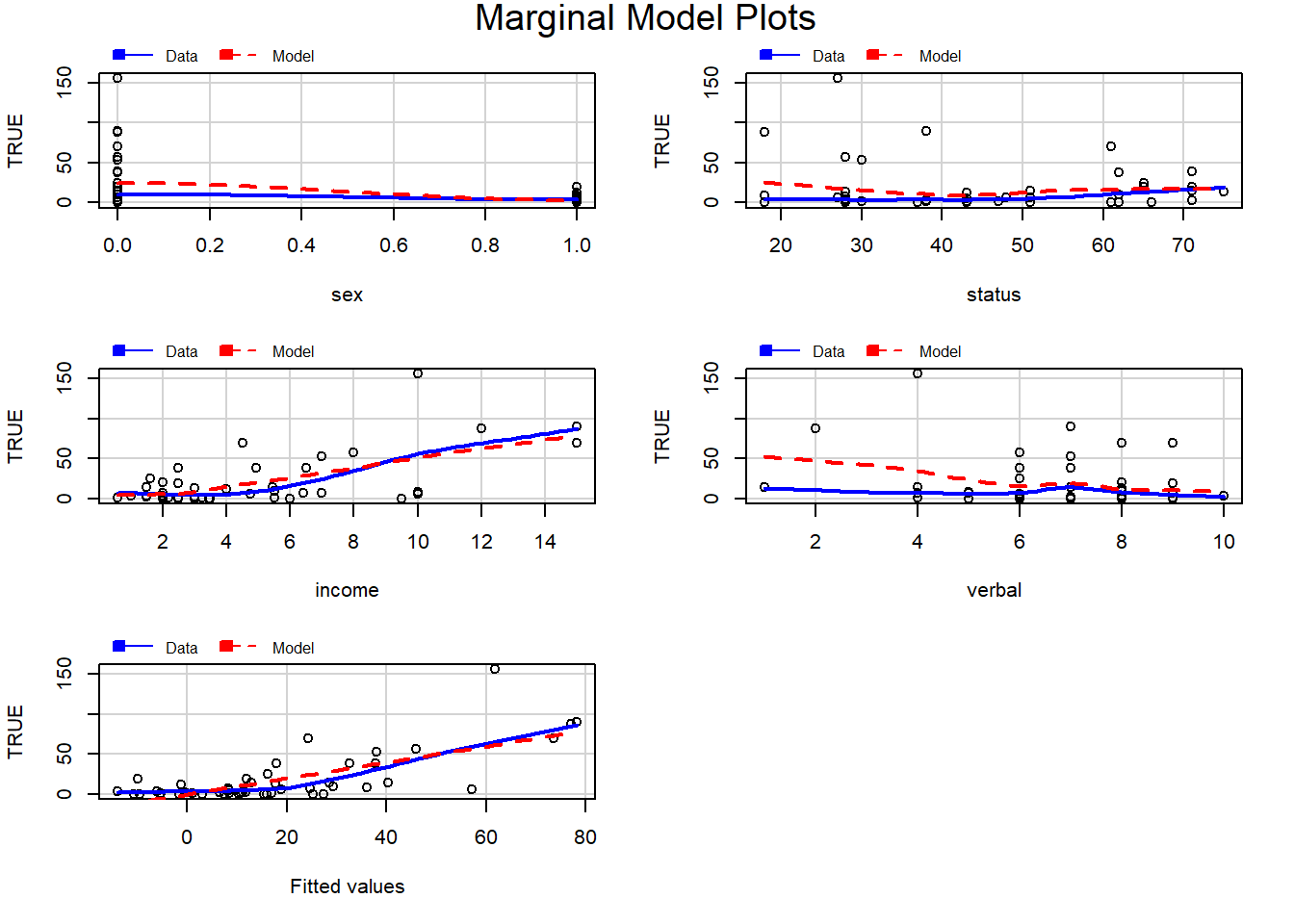
Gráfico de Resíduos vs Variáveis no modelo
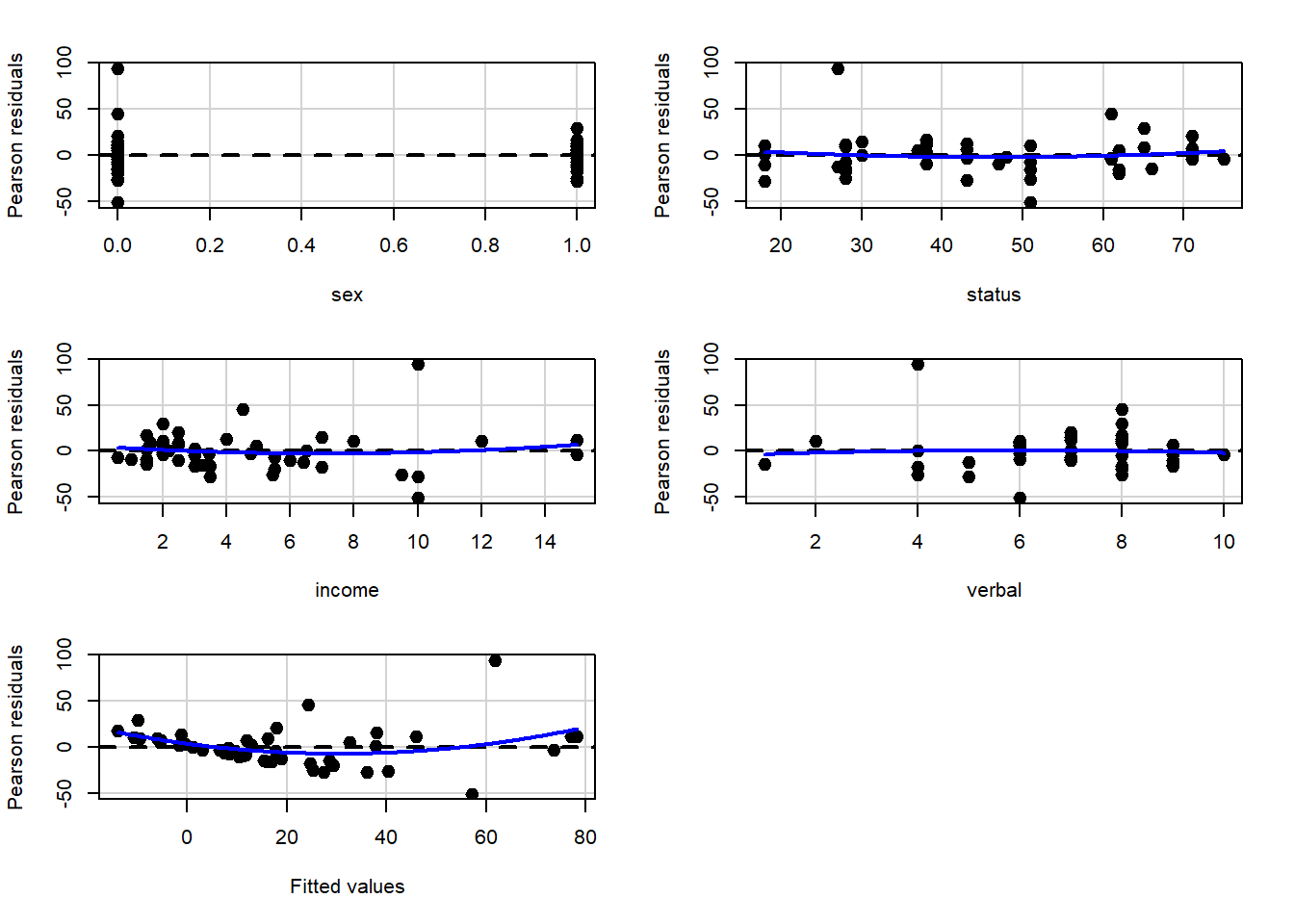
## Test stat Pr(>|Test stat|)
## sex -0.3418 0.734241
## status 0.5854 0.561466
## income 0.6807 0.499908
## verbal -0.2674 0.790538
## Tukey test 2.7242 0.006445 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Diagnóstico de outliers, pontos de alavanca e influência













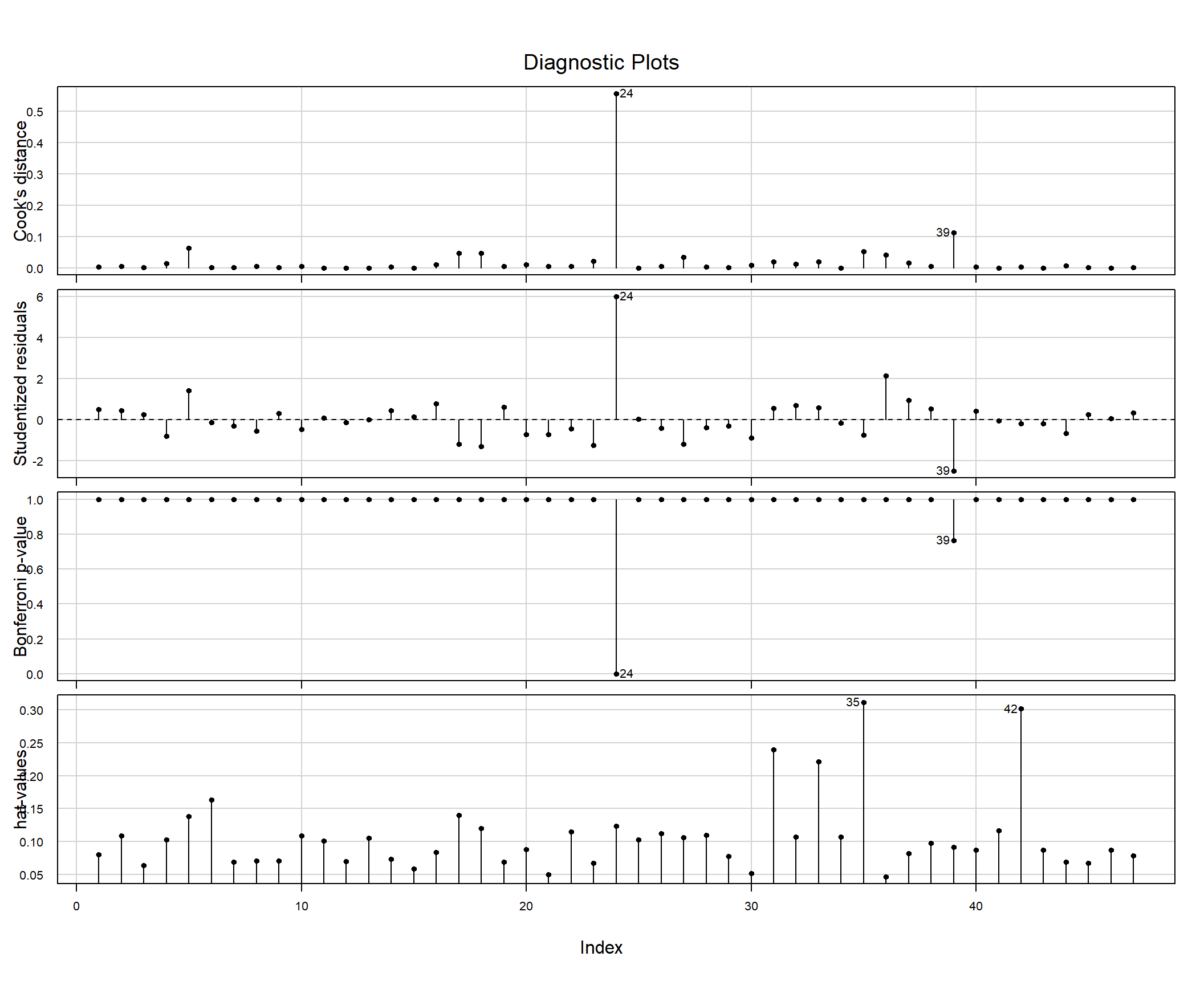
Análise de pontos atípicos
Vamos relevar, por um instante, as demais inadequações do ajuste e nos concentrar no efeito da observação 24, indicada como outlier e observação influente.
## sex status income verbal gamble
## 24 0 27 10 4 156## sex status income verbal
## Min. :0.0000 Min. :18.00 Min. : 0.600 Min. : 1.00
## 1st Qu.:0.0000 1st Qu.:28.00 1st Qu.: 2.000 1st Qu.: 6.00
## Median :0.0000 Median :43.00 Median : 3.250 Median : 7.00
## Mean :0.4043 Mean :45.23 Mean : 4.642 Mean : 6.66
## 3rd Qu.:1.0000 3rd Qu.:61.50 3rd Qu.: 6.210 3rd Qu.: 8.00
## Max. :1.0000 Max. :75.00 Max. :15.000 Max. :10.00
## gamble
## Min. : 0.0
## 1st Qu.: 1.1
## Median : 6.0
## Mean : 19.3
## 3rd Qu.: 19.4
## Max. :156.0Trata-se do adolesente com maior valor gasto em apostas. Vamos reajustar o modelo desconsiderando este indivíduo.
Utilizar o modelo ajuste e retirar a observação 24
Comparar estimativas e erros padrões produzidas pelos dois modelos
## Calls:
## 1: lm(formula = gamble ~ ., data = teengamb)
## 2: lm(formula = gamble ~ ., data = teengamb, subset = -24)
##
## Model 1 Model 2
## (Intercept) 22.56 7.63
## SE 17.20 12.93
##
## sex -22.12 -16.30
## SE 8.21 6.13
##
## status 0.0522 0.1739
## SE 0.2811 0.2083
##
## income 4.962 4.331
## SE 1.025 0.764
##
## verbal -2.96 -1.80
## SE 2.17 1.61
## Nota-se redução expressiva na estimativa referente ao efeito de sexo. Os erros padrões de sexo e income são reduzidos ao desconsiderar o dado sob investigação. De qualquer forma, as conclusões se mantêm com relação aos efeitos significativos e não significativos na análise.
Conferir se a variância está constante
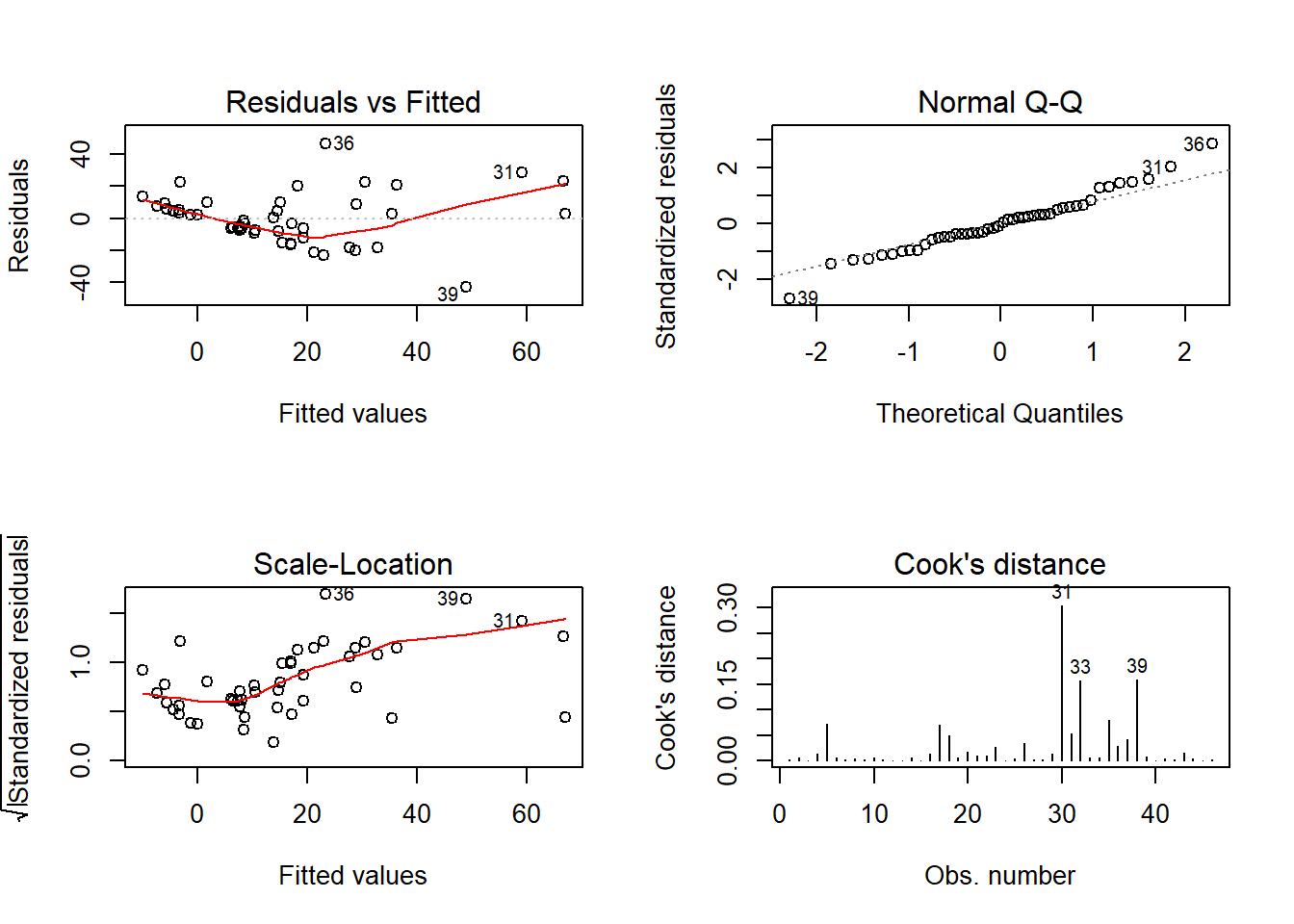
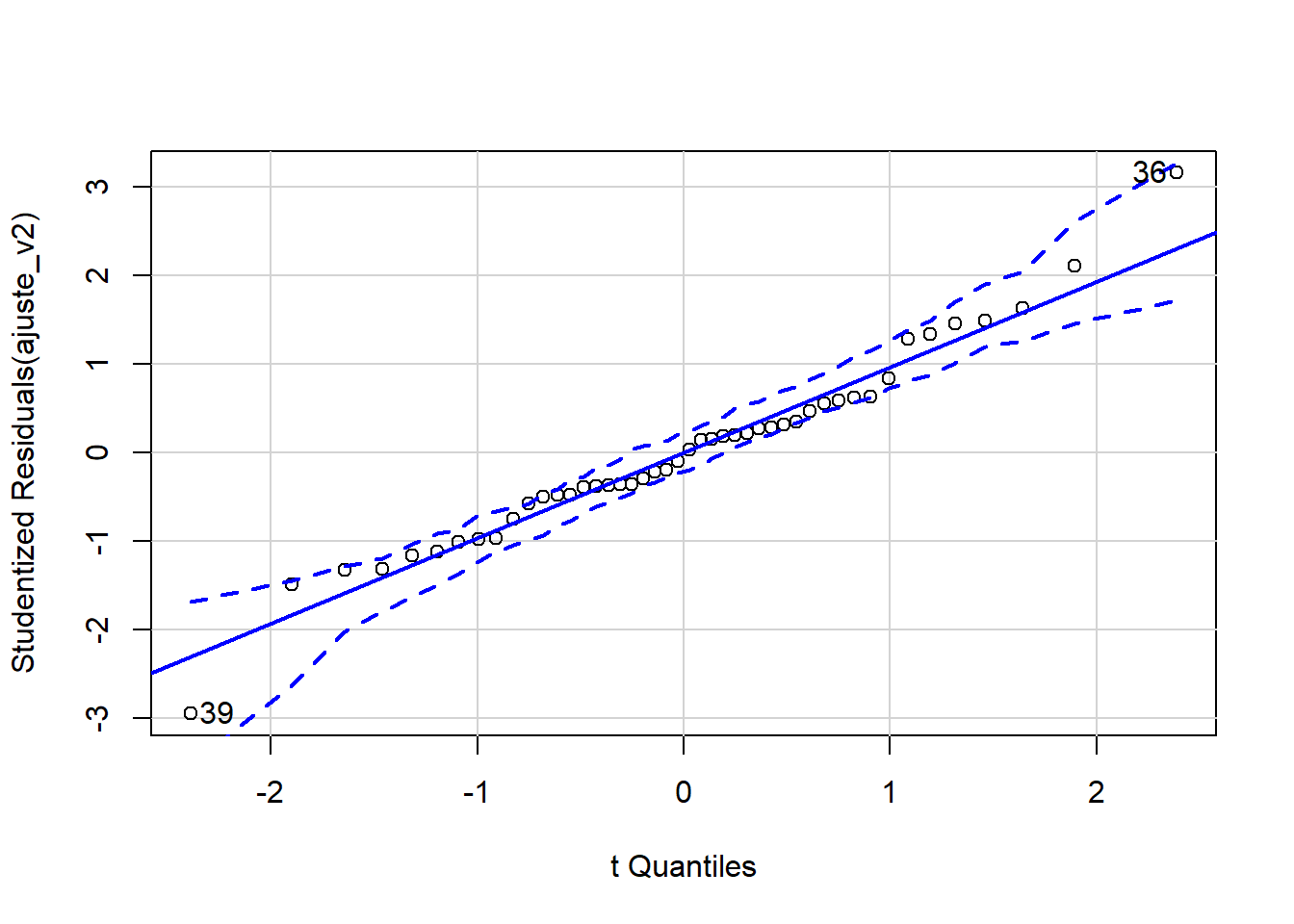
## 36 39
## 35 38Mesmo após a exclusão dos dados do indivíduo 24 os resíduos ainda apresentam variância não constante. Ainda há um resíduo com valor absoluto próximo a 3 que mereceria alguma atenção.
Gráfico para os dfbetas

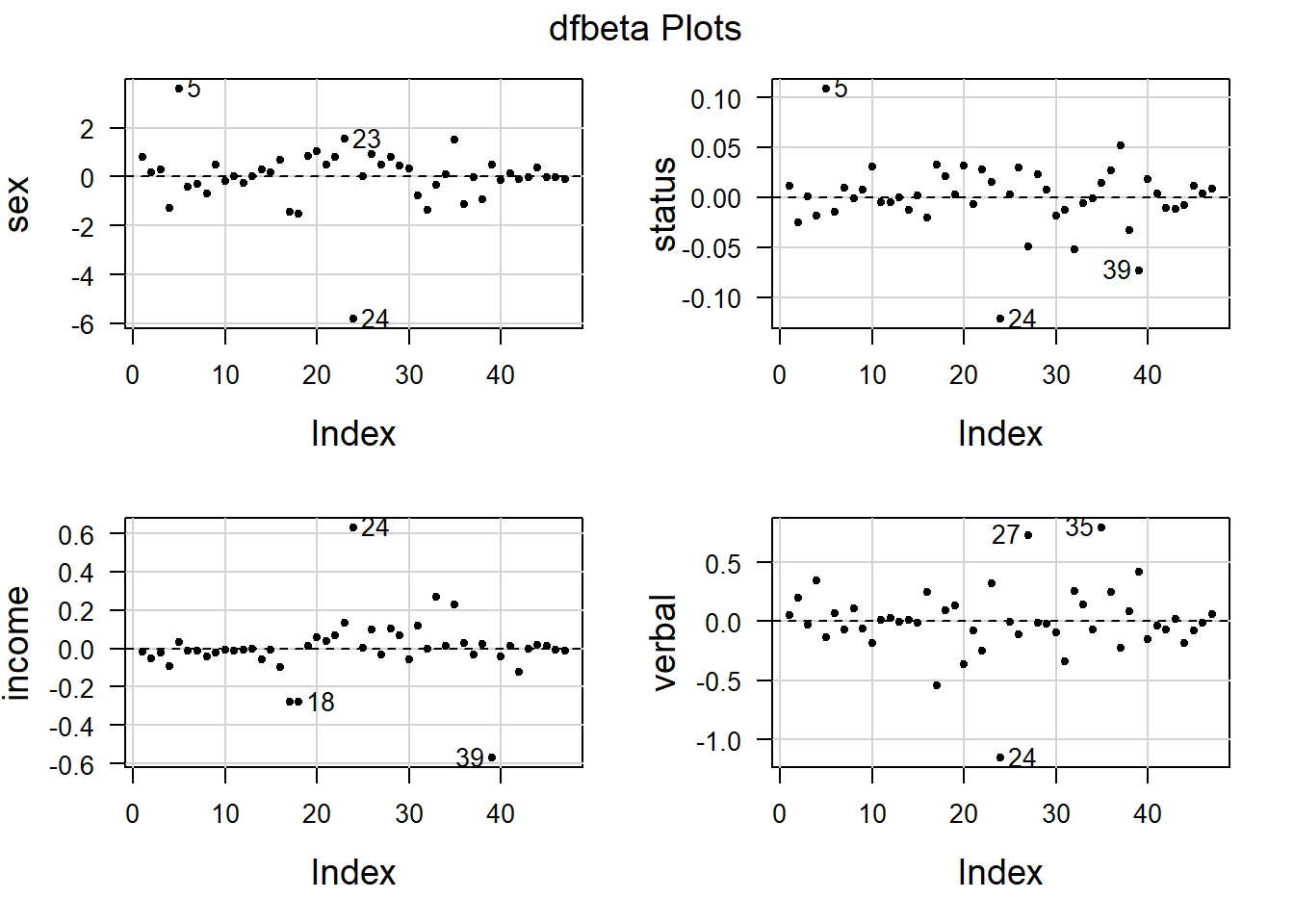
Novamente a observação 24 aparece como potencial ponto influente na estimativa de cada parâmetro do modelo.
## Potentially influential observations of
## lm(formula = gamble ~ ., data = teengamb) :
##
## dfb.1_ dfb.sex dfb.stts dfb.incm dfb.vrbl dffit cov.r cook.d hat
## 24 1.18_* -0.96 -0.59 0.83 -0.72 2.26_* 0.05_* 0.56 0.12
## 31 0.17 -0.09 -0.04 0.12 -0.15 0.31 1.43_* 0.02 0.24
## 33 -0.08 -0.04 -0.02 0.26 0.06 0.31 1.39_* 0.02 0.22
## 35 -0.47 0.18 0.05 0.22 0.36 -0.51 1.53_* 0.05 0.31
## 39 0.11 0.06 -0.28 -0.59 0.20 -0.80 0.61_* 0.11 0.09
## 42 0.08 -0.01 -0.04 -0.12 -0.03 -0.13 1.61_* 0.00 0.30Análise de multicolinearidade





Nosso objetivo aqui é ajustar um modelo de regressão linear considerando a variável hipcenter como resposta e as demais variáveis como explicativas.
Como diagnóstico preliminar de multicolinearidade vamos analisar as correlações bivariadas.
## Age Weight HtShoes Ht Seated Arm Thigh Leg hipcenter
## Age 1.00 0.08 -0.08 -0.09 -0.17 0.36 0.09 -0.04 0.21
## Weight 0.08 1.00 0.83 0.83 0.78 0.70 0.57 0.78 -0.64
## HtShoes -0.08 0.83 1.00 1.00 0.93 0.75 0.72 0.91 -0.80
## Ht -0.09 0.83 1.00 1.00 0.93 0.75 0.73 0.91 -0.80
## Seated -0.17 0.78 0.93 0.93 1.00 0.63 0.61 0.81 -0.73
## Arm 0.36 0.70 0.75 0.75 0.63 1.00 0.67 0.75 -0.59
## Thigh 0.09 0.57 0.72 0.73 0.61 0.67 1.00 0.65 -0.59
## Leg -0.04 0.78 0.91 0.91 0.81 0.75 0.65 1.00 -0.79
## hipcenter 0.21 -0.64 -0.80 -0.80 -0.73 -0.59 -0.59 -0.79 1.00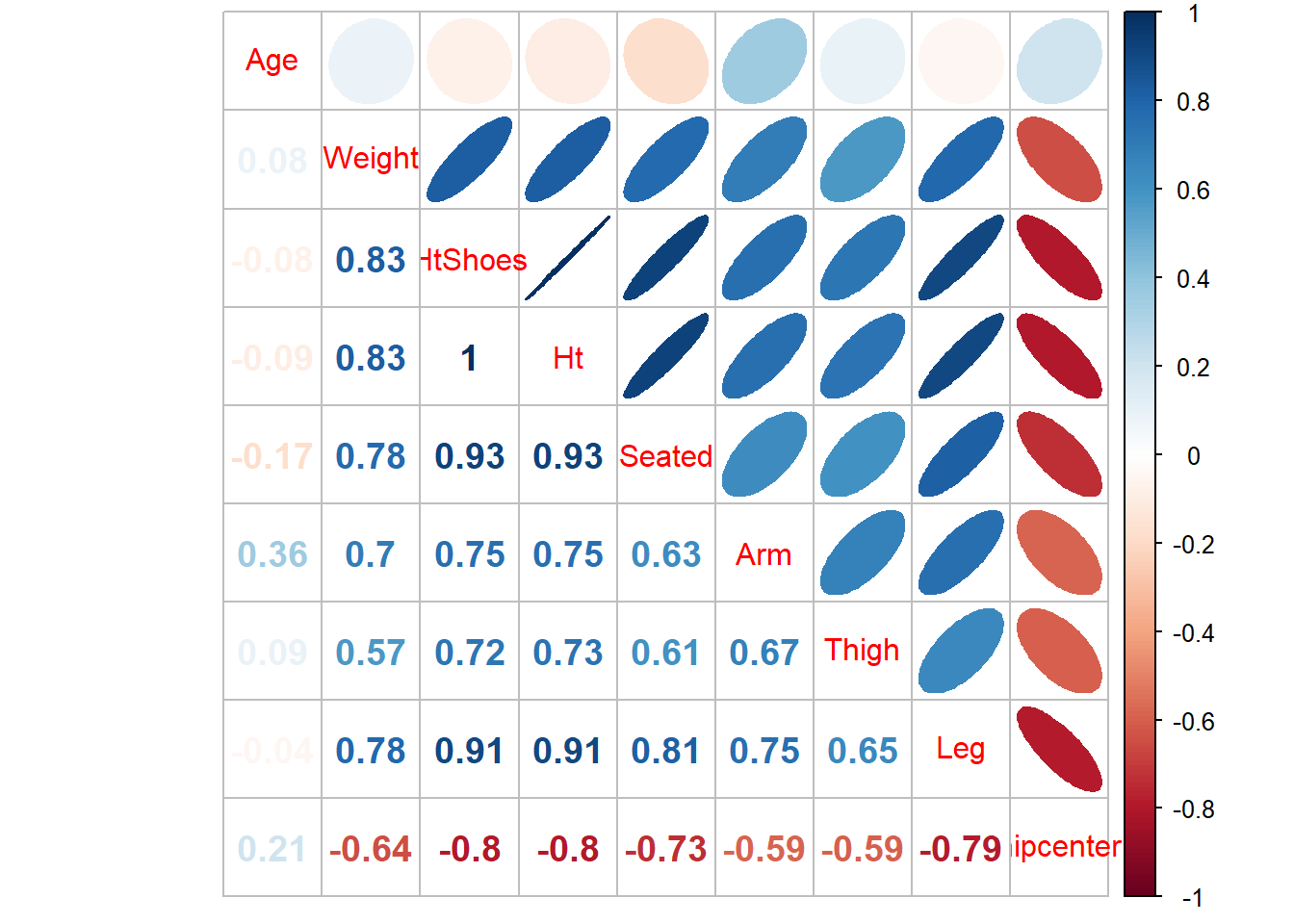
É possível observar correlações lineares bastante fortes entre as covariáveis, algumas delas maiores que 0,90. Fortíssimo indicador de multicolinearidade.
##
## Call:
## lm(formula = hipcenter ~ ., data = seatpos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -73.827 -22.833 -3.678 25.017 62.337
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 436.43213 166.57162 2.620 0.0138 *
## Age 0.77572 0.57033 1.360 0.1843
## Weight 0.02631 0.33097 0.080 0.9372
## HtShoes -2.69241 9.75304 -0.276 0.7845
## Ht 0.60134 10.12987 0.059 0.9531
## Seated 0.53375 3.76189 0.142 0.8882
## Arm -1.32807 3.90020 -0.341 0.7359
## Thigh -1.14312 2.66002 -0.430 0.6706
## Leg -6.43905 4.71386 -1.366 0.1824
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 37.72 on 29 degrees of freedom
## Multiple R-squared: 0.6866, Adjusted R-squared: 0.6001
## F-statistic: 7.94 on 8 and 29 DF, p-value: 1.306e-05Embora as correlações bivariadas entre a resposta e as explicativas sejam numericamente bastante elevadas, o modelo ajustado não indica significância para nenhuma variável explicativa. Esse resultado é contraditório, ainda, com o valor do \(R^2\) (0.687), que é bastante expressivo e pouco compatível com um modelo sem qualquer variável associada à resposta.
Valores de VIF
Na mão:
ajuste_Leg <- lm(Leg ~ Age + Weight + HtShoes + Ht + Seated + Arm + Thigh, data = seatpos)
R2 <- summary(ajuste_Leg)$r.squared
vif_Leg <- (1/(1-R2)) ## Age Weight HtShoes Ht Seated Arm
## 1.997931 3.647030 307.429378 333.137832 8.951054 4.496368
## Thigh Leg
## 2.762886 6.694291Há muita colinearidade nos dados. Se extrairmos a raiz quadrada de qualquer um desses valores, teremos quantas vezes o respectivo erro padrão é maior do que aquele que teríamos se as variáveis fossem ortogonais.
## Age Weight HtShoes Ht Seated Arm Thigh
## 1.413482 1.909720 17.533664 18.252064 2.991831 2.120464 1.662193
## Leg
## 2.587333Para avlaiar o efeito da multicolinearidade, vamos perturbar levemente a variável resposta, adicionando erros aleatórios com distribuição Normal(0 , 5) a cada valor de y.
Modelo 2 - Perturbação na variável resposta
##
## Call:
## lm(formula = hipcenter + rnorm(38, 0, 5) ~ ., data = seatpos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -74.937 -23.906 -3.469 22.328 62.685
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 419.204055 172.121150 2.436 0.0213 *
## Age 0.822678 0.589330 1.396 0.1733
## Weight 0.009488 0.341997 0.028 0.9781
## HtShoes -4.998022 10.077969 -0.496 0.6237
## Ht 2.940552 10.467363 0.281 0.7808
## Seated 0.866636 3.887226 0.223 0.8251
## Arm -1.106140 4.030137 -0.274 0.7857
## Thigh -1.458802 2.748646 -0.531 0.5996
## Leg -6.607300 4.870908 -1.356 0.1854
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 38.98 on 29 degrees of freedom
## Multiple R-squared: 0.6689, Adjusted R-squared: 0.5776
## F-statistic: 7.324 on 8 and 29 DF, p-value: 2.693e-05##
## Call:
## lm(formula = hipcenter ~ ., data = seatpos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -73.827 -22.833 -3.678 25.017 62.337
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 436.43213 166.57162 2.620 0.0138 *
## Age 0.77572 0.57033 1.360 0.1843
## Weight 0.02631 0.33097 0.080 0.9372
## HtShoes -2.69241 9.75304 -0.276 0.7845
## Ht 0.60134 10.12987 0.059 0.9531
## Seated 0.53375 3.76189 0.142 0.8882
## Arm -1.32807 3.90020 -0.341 0.7359
## Thigh -1.14312 2.66002 -0.430 0.6706
## Leg -6.43905 4.71386 -1.366 0.1824
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 37.72 on 29 degrees of freedom
## Multiple R-squared: 0.6866, Adjusted R-squared: 0.6001
## F-statistic: 7.94 on 8 and 29 DF, p-value: 1.306e-05Embora o \(R^2\) dos dois modelos seja praticamente o mesmo, percebe-se uma boa variação nas estimativas pontuais geradas pelos dois modelos. Esse tipo de comportamento frente a pequenas perturbações nos dados é típico em casos de multicolinearidade. Com exceção da idade, as demais variáveis explicativas estão, em geral, fortemente correlacionadas. O que aconteceria se usássemos apenas uma delas na especificação do modelo? Vamos considerar a altura aferida com o indivíduo descalço.
Modelo 3 - regressão linear simples
##
## Call:
## lm(formula = hipcenter ~ Ht, data = seatpos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -99.956 -27.850 5.656 20.883 72.066
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 556.2553 90.6704 6.135 4.59e-07 ***
## Ht -4.2650 0.5351 -7.970 1.83e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 36.37 on 36 degrees of freedom
## Multiple R-squared: 0.6383, Adjusted R-squared: 0.6282
## F-statistic: 63.53 on 1 and 36 DF, p-value: 1.831e-09A associação entre a altura e a variável resposta é altamente significativa. Além disso, a variação no coeficiente de determinação, resultante da eliminação de todas as outras variáveis, foi bem pequena. Algo semelhante ocorreria se escolhessemos alguma outra variável ao invés de Ht. Fica como exercício. Vamos usar a técnica de análise de componentes principais para encontrar uma (ou poucas) combinações lineares ortogonais das variáveis explicativas que conservem a maior parte possível da variação dos dados.
O argumento cor = T serve para executar a análise com base nos dados padronizados. NA ACP, isso é importante devido às diferentes escalas das variáveis.
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4
## Standard deviation 2.3818450 1.1121088 0.68098711 0.49087508
## Proportion of Variance 0.7091482 0.1545983 0.05796793 0.03011979
## Cumulative Proportion 0.7091482 0.8637465 0.92171439 0.95183418
## Comp.5 Comp.6 Comp.7 Comp.8
## Standard deviation 0.44070349 0.37306059 0.224375861 0.0398527115
## Proportion of Variance 0.02427745 0.01739678 0.006293066 0.0001985298
## Cumulative Proportion 0.97611163 0.99350840 0.999801470 1.0000000000O primeiro componente explica 70.9% da variação original dos dados; o segundo componente explica 15,4% e, somados, os dois explicam 86,3% da variação total.
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## Age 0.876 0.164 0.165 0.335 0.255
## Weight 0.367 0.430 0.600 -0.554
## HtShoes 0.411 -0.106 0.220 0.537 -0.692
## Ht 0.412 -0.112 0.189 0.509 0.721
## Seated 0.381 -0.218 0.171 0.150 0.617 -0.230 -0.567
## Arm 0.349 0.374 -0.554 -0.238 -0.608
## Thigh 0.328 0.125 -0.862 0.312 -0.104 -0.145
## Leg 0.390 0.117 -0.430 -0.221 0.703 -0.321
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## Proportion Var 0.125 0.125 0.125 0.125 0.125 0.125 0.125 0.125
## Cumulative Var 0.125 0.250 0.375 0.500 0.625 0.750 0.875 1.000As cargas (loadings) dos componentes correspondem aos coeficientes das combinações lineares. Assim, o primeiro componente é praticamente uma média aritmética de todas as variáveis explicativas, com exceção da idade. É um componente referente ao tamanho do motorista, de forma geral. No segundo componente o coeficiente correspondente à idade é muito maior que os demais, de forma que esse componente expressa, de forma predominante, a idade dos motoristas.
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 1 3.4911907 0.63044905 -0.6458071 -0.09591629 0.44570887 0.40843490
## 2 -0.6388676 0.09514266 0.4627576 -0.10269656 -1.15719897 -0.15065776
## 3 -3.7931332 -0.84557487 -0.7829229 0.35153482 0.03460612 0.08482316
## 4 3.9029053 -0.96067938 -0.5369357 -0.52832731 0.10139621 -0.45410122
## 5 0.7644369 -1.30904590 -0.1819518 0.53859884 0.63525066 0.25475659
## Comp.7 Comp.8
## 1 -0.06019110 0.000245038
## 2 0.31568209 0.007890707
## 3 -0.17216322 0.043066971
## 4 -0.03950468 -0.055263885
## 5 -0.10064334 -0.099924556Os escores são os valores dos componentes calculados para cada indivíduo.
## Comp.1 Comp.2 Comp.3 Comp.4
## Comp.1 1.000000e+00 9.393495e-17 -7.932111e-16 -2.056704e-16
## Comp.2 9.393495e-17 1.000000e+00 1.126261e-17 -3.302737e-16
## Comp.3 -7.932111e-16 1.126261e-17 1.000000e+00 -2.604603e-16
## Comp.4 -2.056704e-16 -3.302737e-16 -2.604603e-16 1.000000e+00
## Comp.5 4.978819e-16 -2.221649e-16 -2.052937e-17 1.996025e-15
## Comp.5 Comp.6 Comp.7 Comp.8
## Comp.1 4.978819e-16 1.664879e-17 3.458316e-15 -1.904163e-14
## Comp.2 -2.221649e-16 -2.208141e-16 -5.035650e-16 1.493032e-15
## Comp.3 -2.052937e-17 7.842771e-16 1.079113e-15 -7.794370e-16
## Comp.4 1.996025e-15 3.581087e-16 1.973883e-15 -8.433193e-15
## Comp.5 1.000000e+00 -1.205926e-15 -1.505442e-16 -8.988269e-15Observe que os escores são ortogonais.
Vamos fazer um novo ajuste do modelo de regressão agora substituindo as variáveis originais pelos escores dos dois componentes principais.
Modelo 4
seatpos_novo <- data.frame(seatpos$hipcenter, scores[,1:2])
ajuste_pca <- lm(seatpos.hipcenter ~ ., data = seatpos_novo)
summary(ajuste_pca)##
## Call:
## lm(formula = seatpos.hipcenter ~ ., data = seatpos_novo)
##
## Residuals:
## Min 1Q Median 3Q Max
## -84.643 -25.582 -0.743 24.887 61.798
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -164.885 5.772 -28.568 < 2e-16 ***
## Comp.1 -19.440 2.423 -8.022 1.93e-09 ***
## Comp.2 11.171 5.190 2.153 0.0383 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 35.58 on 35 degrees of freedom
## Multiple R-squared: 0.6634, Adjusted R-squared: 0.6442
## F-statistic: 34.5 on 2 and 35 DF, p-value: 5.292e-09Observe que ambos os componentes estão associados de forma significativa à posição de dirigir. Além disso, o \(R^2\) e a significância do modelo ajustado são bastante próximos aos do modelo original.