Análise de deviance

Avaliação da qualidade do ajuste usando simulação (ilustração). Ao invés de utilizar a distribuição qui-quadrado assintótica como referência para testar a qualidade do ajuste com base na deviance, vamos obter a distribuição de referência para o teste via simulação.

Passo 1: Ajuste do modelo aos dados observados

dados1 <- read.csv2('sinistros.csv')[,-1]
head(dados1)

##   idade sexo    usop anosest claims
## 1    41  Fem Estrada      10      3
## 2    39 Masc  Cidade      16      0
## 3    46 Masc Estrada       5      1
## 4    45  Fem  Cidade       9      0
## 5    41  Fem  Cidade      12      1
## 6    33 Masc Estrada       8      7

ajuste1 <- glm(claims ~ ., family = poisson, data = dados1) 
# Ajuste do GLM do número de sinistros pelo resto.

print(ajuste1) 

## 
## Call:  glm(formula = claims ~ ., family = poisson, data = dados1)
## 
## Coefficients:
## (Intercept)        idade     sexoMasc  usopEstrada      anosest  
##    2.699698    -0.058708    -0.016386     0.257935    -0.004463  
## 
## Degrees of Freedom: 499 Total (i.e. Null);  495 Residual
## Null Deviance:       733.8 
## Residual Deviance: 581.5     AIC: 1579

# Resumo do modelo ajustado

fit <- fitted(ajuste1); head(fit, n = 10) 

##         1         2         3         4         5         6         7 
## 1.6585675 1.3802570 1.2440128 1.0178051 1.2700958 2.6331007 0.9792632 
##         8         9        10 
## 1.1783287 1.3499300 1.6099097

# Valores ajustados pelo modelo para cada indivíduo na amostra.

fit1 <- fitted(ajuste1)[1]; fit1 

##        1 
## 1.658567

# Valor ajustado pelo modelo para o primeiro indivíduo na amostra

devobs <- ajuste1$deviance; devobs 

## [1] 581.5254

# devobs armazena o desvio avaliado para o ajuste com os dados observados.

Passo 2: Simulação de y com base no modelo ajustado.

yest1 <- rpois(1,fit1); yest1 

## [1] 0

# Número de sinistros simulado para o 1º indivíduo com base no modelo ajustado. 

yest <- rpois(500,fit); yest 

##   [1] 2 3 1 0 1 1 0 1 3 2 1 0 0 3 3 2 2 4 1 1 2 0 0 3 0 1 1 0 2 2 3 1 1 0 3
##  [36] 1 1 2 2 4 2 0 3 3 1 3 3 1 2 0 1 1 2 1 3 4 2 0 1 2 0 1 2 1 6 2 4 0 1 4
##  [71] 8 1 0 1 1 0 0 5 3 1 3 3 3 0 3 1 0 0 4 1 0 2 3 5 0 2 1 2 4 1 6 1 3 2 1
## [106] 0 5 1 2 1 1 2 0 2 0 1 1 0 1 2 2 0 0 0 4 3 2 3 1 3 2 1 5 3 3 4 2 1 3 2
## [141] 7 4 0 2 0 0 1 1 0 1 1 3 0 0 2 0 6 1 0 1 1 2 2 3 0 3 4 3 1 1 1 1 1 1 1
## [176] 1 2 2 1 1 1 2 1 2 1 3 2 0 0 1 0 0 4 2 1 1 2 1 4 3 3 3 8 2 5 0 0 0 2 0
## [211] 4 3 1 2 1 1 2 1 0 2 0 2 3 3 4 1 1 1 2 0 1 4 1 0 0 0 0 1 3 4 7 0 4 0 2
## [246] 2 4 0 2 5 0 2 1 1 4 2 4 2 2 1 0 2 3 2 0 4 3 3 4 2 6 5 0 2 4 0 1 3 2 2
## [281] 3 1 1 1 4 1 1 2 1 3 1 2 5 1 7 2 0 1 5 0 2 1 3 3 2 2 0 0 1 1 2 0 1 1 5
## [316] 3 1 3 3 6 2 1 2 2 2 2 1 2 1 1 1 3 0 3 1 2 3 2 3 1 4 0 2 0 2 3 0 0 1 4
## [351] 4 1 1 1 2 0 5 4 2 0 5 4 1 1 5 0 1 0 0 2 1 1 1 3 1 3 2 2 4 2 1 0 2 3 0
## [386] 1 2 2 4 0 3 1 1 2 2 1 2 0 3 5 2 0 2 4 4 3 3 1 2 4 2 5 2 4 1 1 4 1 3 1
## [421] 3 3 3 2 2 1 0 1 0 2 1 0 1 2 4 6 0 0 5 1 2 4 0 2 1 1 0 2 0 6 1 0 0 3 1
## [456] 3 0 2 3 2 1 4 0 0 2 1 2 3 1 6 6 2 4 3 2 1 3 5 1 0 2 1 0 2 0 2 4 4 0 2
## [491] 1 1 6 2 5 1 2 1 0 5

# Números de sinistros simulados para os 500 indivíduo da amostra com 
# base no modelo ajustado.

Passo 3: Ajuste do GLM aos dados simulados.

ajuste1est <- glm(yest ~ ., family = poisson, data = dados1)

dev1 <- ajuste1est$deviance; dev1 

## [1] 551.165

# dev1 armazena a deviance avaliada para o ajuste com os dados simulados

Passo 4: Simulação dos passos 2 e 3 por 1000 vezes

desviossim <- numeric() 
# desviossim vai armazenar os desvios gerados nas 1000 simulações.

desviossim[1] <- dev1 
# Armazenando a primeira simulação.

for(i in 2:1000){
     
     yest <- rpois(500,fit) 
     
     ajuste1est <- glm(yest ~ ., family = poisson, data = dados1)
     desviossim[i] <- ajuste1est$deviance 
}

head(desviossim, n = 10)

##  [1] 551.1650 518.9360 574.0000 519.9429 551.7603 579.2768 572.7113
##  [8] 541.3222 622.4476 552.7068

Antes do passo 5, vamos sobrepor a distribuição simulada para os desvios e a distribuição qui-quadrado (n-p)

hist(desviossim, freq=F, xlim=c(300,700))
curve(dchisq(x,495), from=300, to=700, add = T)

# Claramente, a aproximação com a distribuição qui-quadrado é bem ruim

lines(c(devobs,devobs), c(0,1), lty=2, col='red')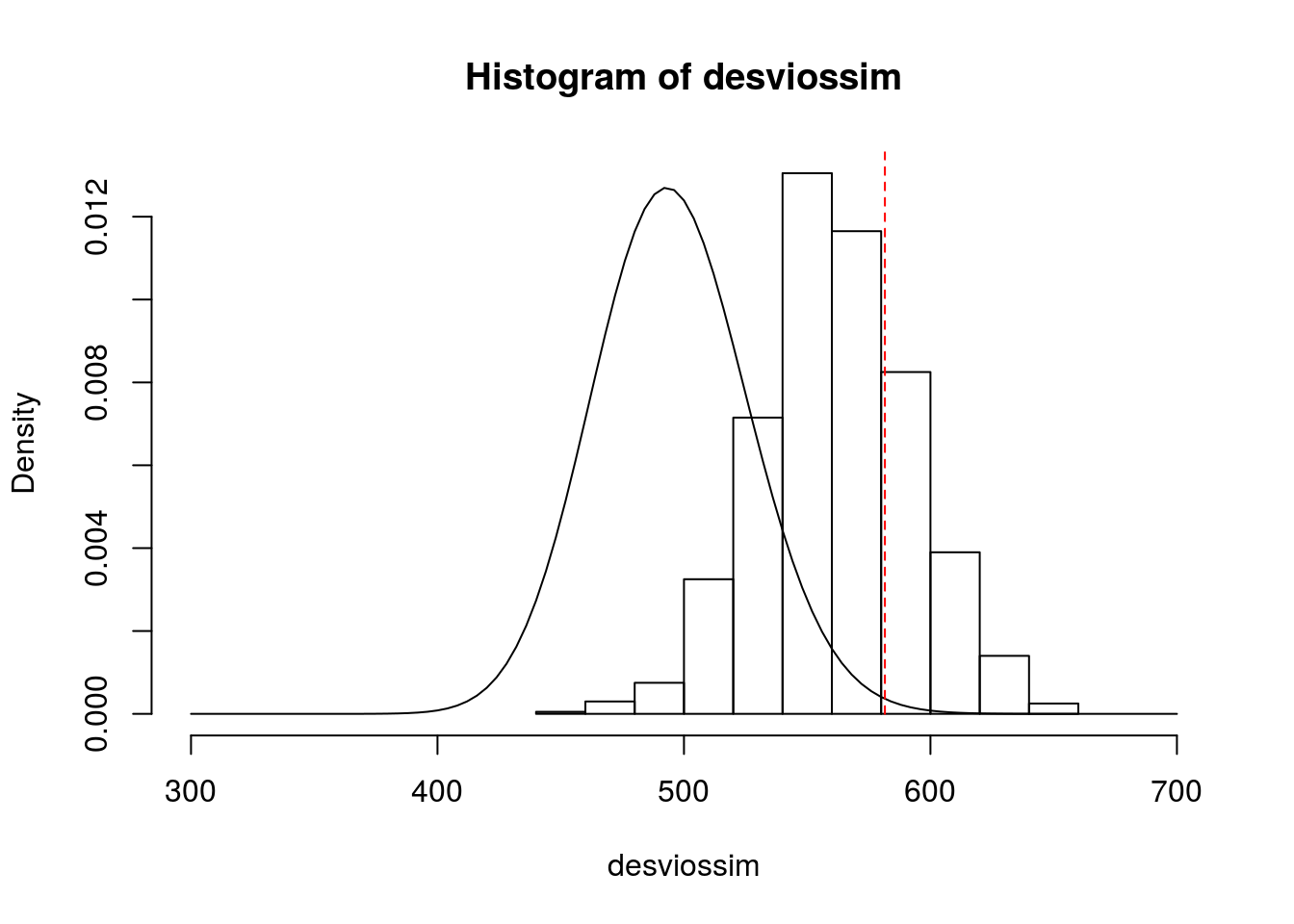 

Representando o valor observado para a deviance.

Passo 5: Obtendo o p-value

psimulado <- sum(desviossim > devobs)/1000; psimulado 

## [1] 0.249

Logo, não há evidências de que o modelo esteja mal ajustado.

Já se usássemos a aproximação com a distribuição qui-quadrado:

paproximado <- pchisq(devobs,495,lower.tail=F); paproximado 

## [1] 0.004329773

Pela aproximação com a qui-quadrado, rejeitariamos o modelo.

Segundo exemplo

Vamos ver um segundo exemplo, em que as contagens (e as médias) são maiores.

Gerando valores para x e y

set.seed(4159)
x <- round(rnorm(500, 10, 2))
y <- rpois(500, exp(x))

ajuste1 <- glm(y ~ x, family = poisson)
fit1 <- fitted(ajuste1)
devobs <- ajuste1$deviance

desviossim <- numeric()

for(i in 1:1000){
     
     yest=rpois(500,fit1) 
     
     ajuste1est=glm(yest~x,family=poisson)
     desviossim[i]=ajuste1est$deviance 
}

head(desviossim, n = 10)

##  [1] 503.7914 487.0985 474.3885 459.2264 476.6905 484.1637 511.5090
##  [8] 466.4037 455.8270 484.5088

hist(desviossim, freq = F, xlim = c(300,700))
curve(dchisq(x,498), from=300, to=700, add=T)
lines(c(devobs, devobs), c(0,1),lty = 2,col = 'red')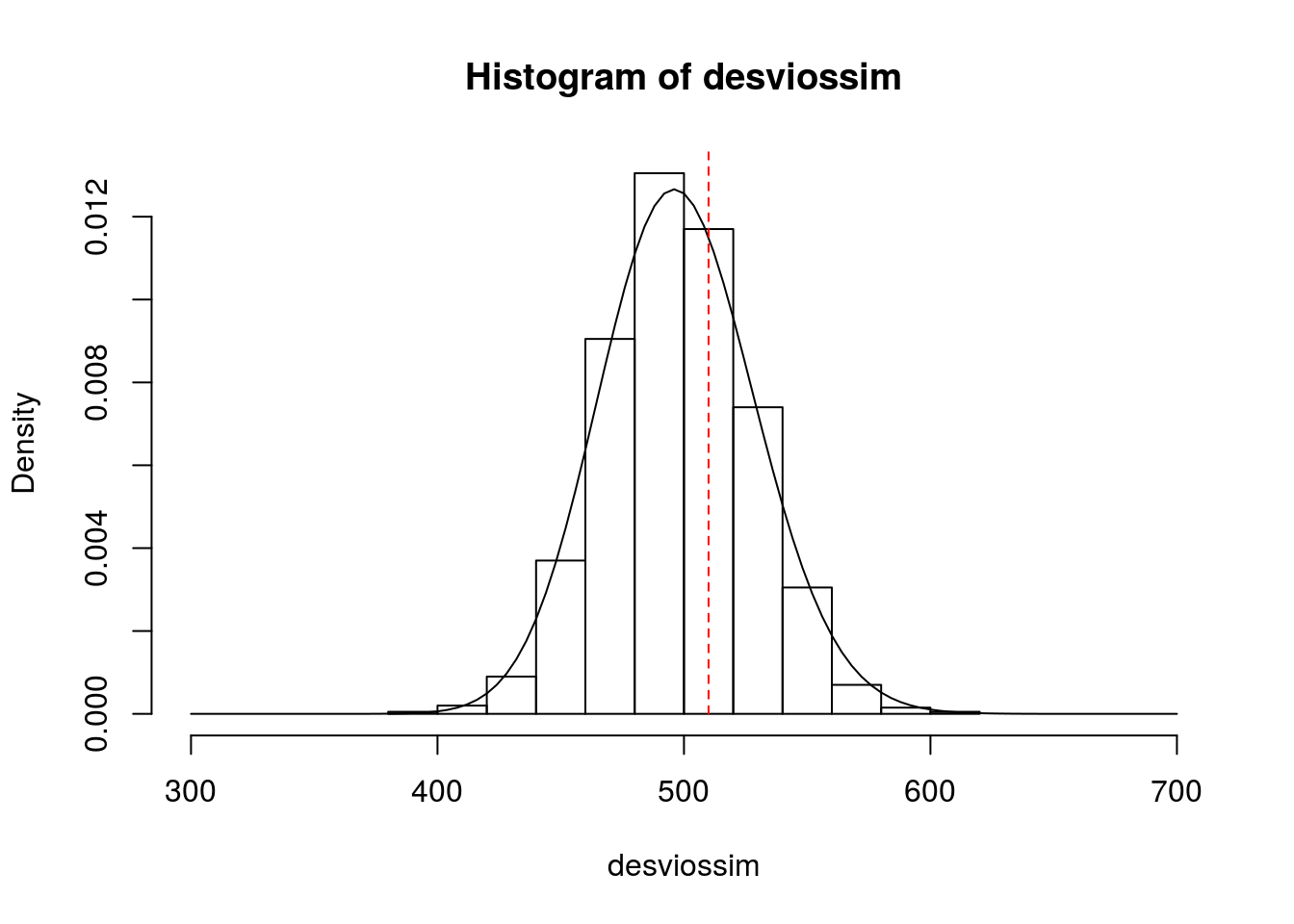 

# Representando o valor observado para a deviance.

psimulado <- sum(desviossim>devobs)/1000; psimulado 

## [1] 0.337

# Logo, não há evidências de que o modelo esteja mal ajustado.

# Já se usássemos a aproximação com a distribuição qui-quadrado:

paproximado <- pchisq(devobs, 495, lower.tail = F); paproximado 

## [1] 0.3112201

# A conclusão usando a aproximação qui-quadrado é semelhante à obtida 
# 3 via simulação.