Executivos compartilhados

require(car) 
require(MASS)
require(lme4)
require(hnp)

help("Ornstein")
data(Ornstein)
head(Ornstein) 

##   assets sector nation interlocks
## 1 147670    BNK    CAN         87
## 2 133000    BNK    CAN        107
## 3 113230    BNK    CAN         94
## 4  85418    BNK    CAN         48
## 5  75477    BNK    CAN         66
## 6  40742    FIN    CAN         69

summary(Ornstein)

##      assets           sector   nation      interlocks    
##  Min.   :    62   MIN    :54   CAN:117   Min.   :  0.00  
##  1st Qu.:   519   MAN    :48   OTH: 18   1st Qu.:  3.00  
##  Median :  1397   AGR    :47   UK : 17   Median :  9.00  
##  Mean   :  5978   FIN    :22   US : 96   Mean   : 13.58  
##  3rd Qu.:  4326   MER    :20             3rd Qu.: 18.00  
##  Max.   :147670   WOD    :19             Max.   :107.00  
##                   (Other):38

Variáveis: assets: ativos da corporação (em milhões de dolares);
sector: setor de operação (AGR: agriculture; TRN: transportes; MIN: mineração, metais,…
nation: CAN: Canadá; UK: Reino Unido; US: Estados Unidos; OTH: outro.
interlocks: Número de diretores e executivos compartilhados com outras companhias.

Objetivo: modelar interlocks em função das demais variáveis.

Alguns gráficos

boxplot(Ornstein$assets) 

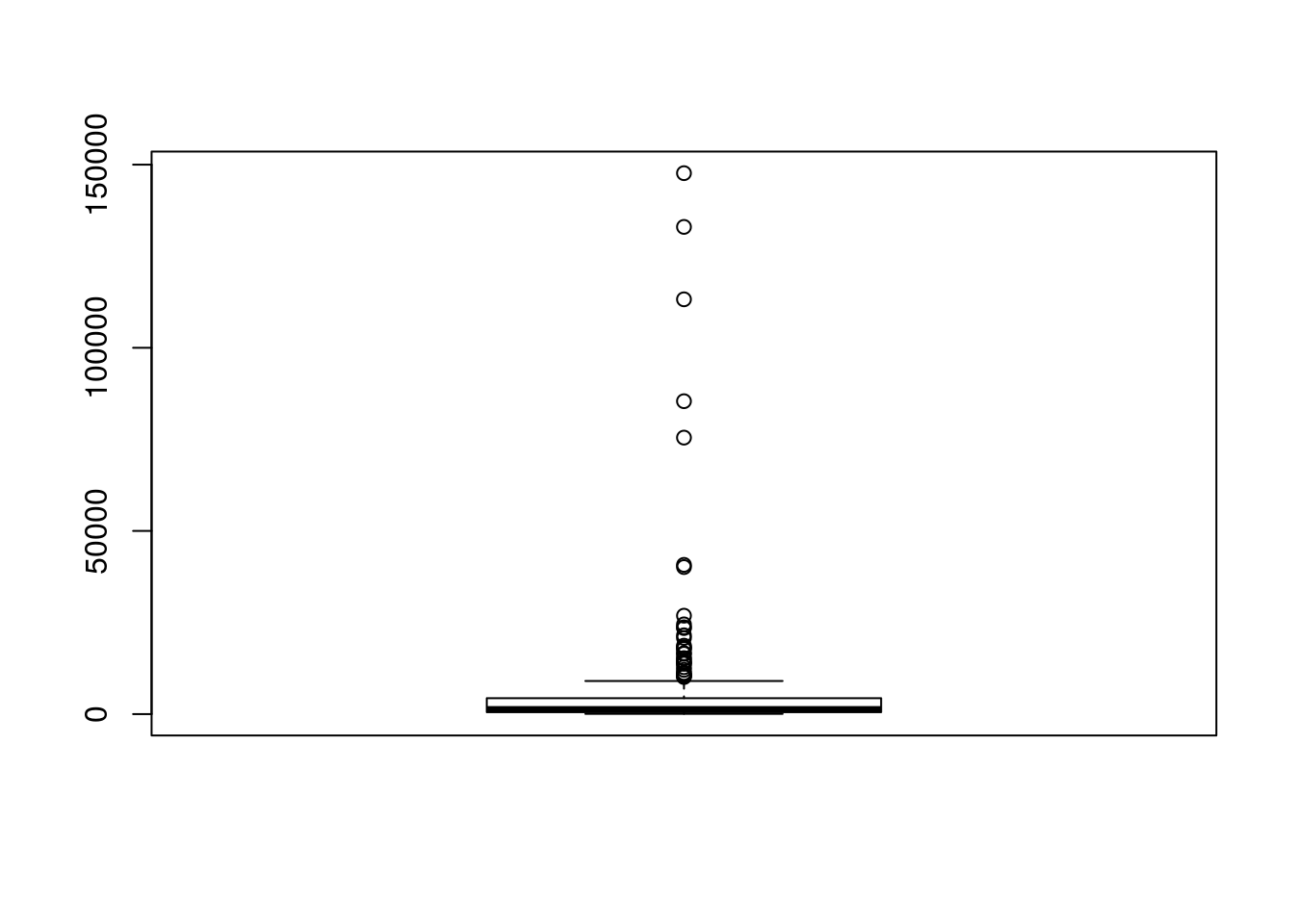
Distribuição dos ativos extremamente assimétrica, com algumas companhias bastante discrepantes (superiores, em relação aos ativos) em relação às demais.

boxplot(log(Ornstein$assets)) 

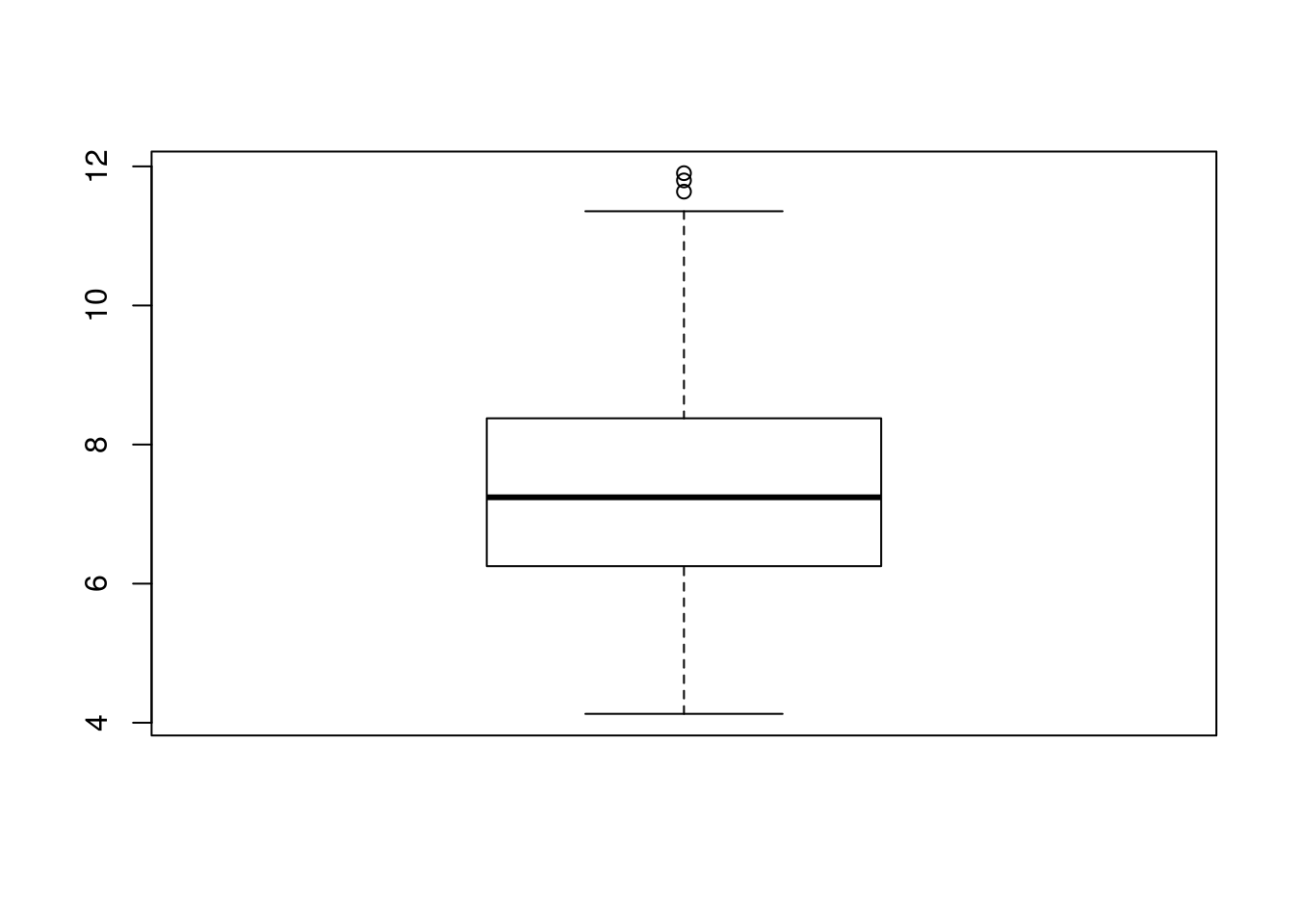
Utilizar o logaritmo simetriza a distribuição dos ativos. Com base nisso, vamos usar log(assets) no modelo.

plot(log(Ornstein$assets),Ornstein$interlocks,pch=20,
     ylab='Número de diretores compartilhados',xlab='Ativos (em milhões de dolares)')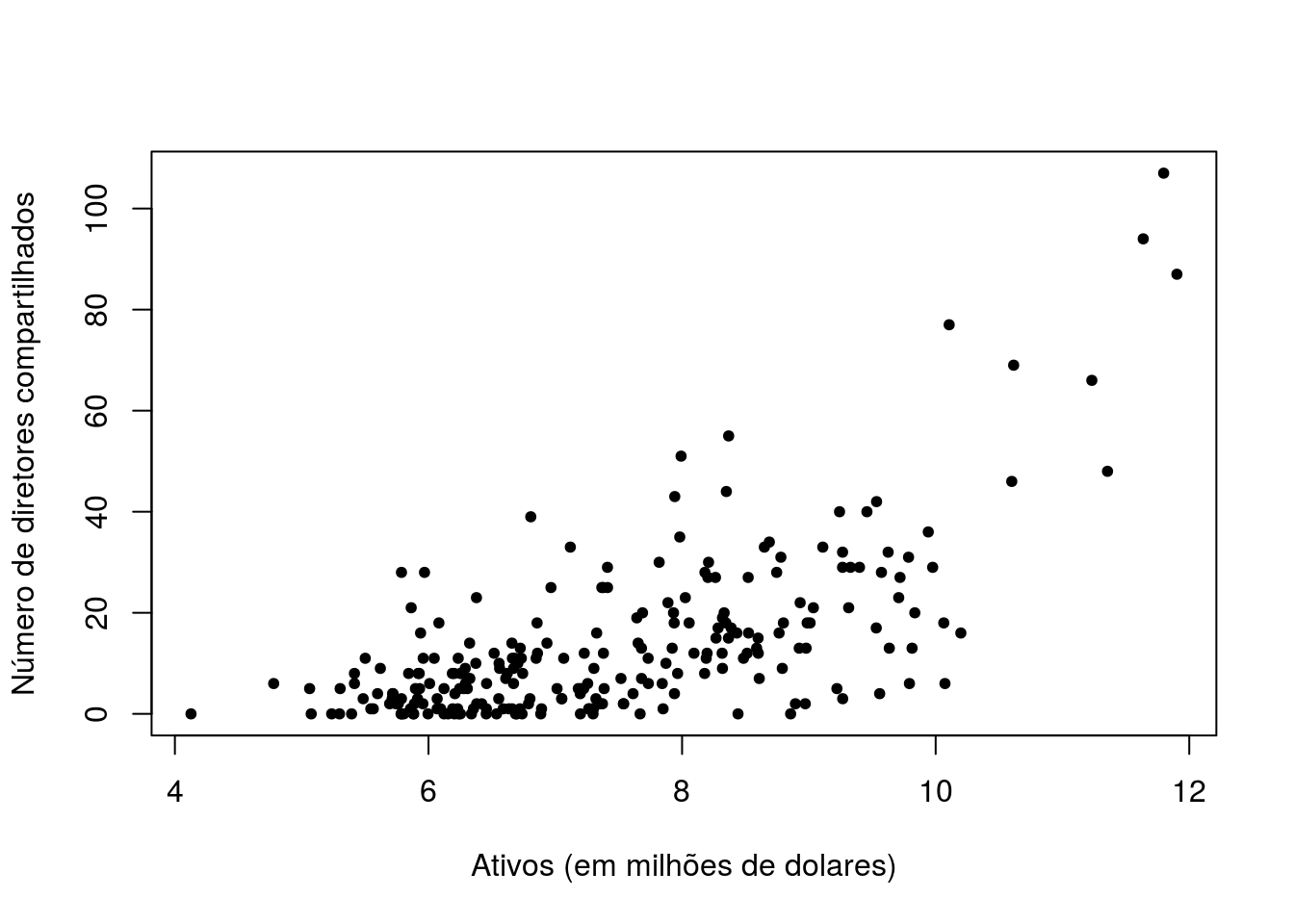

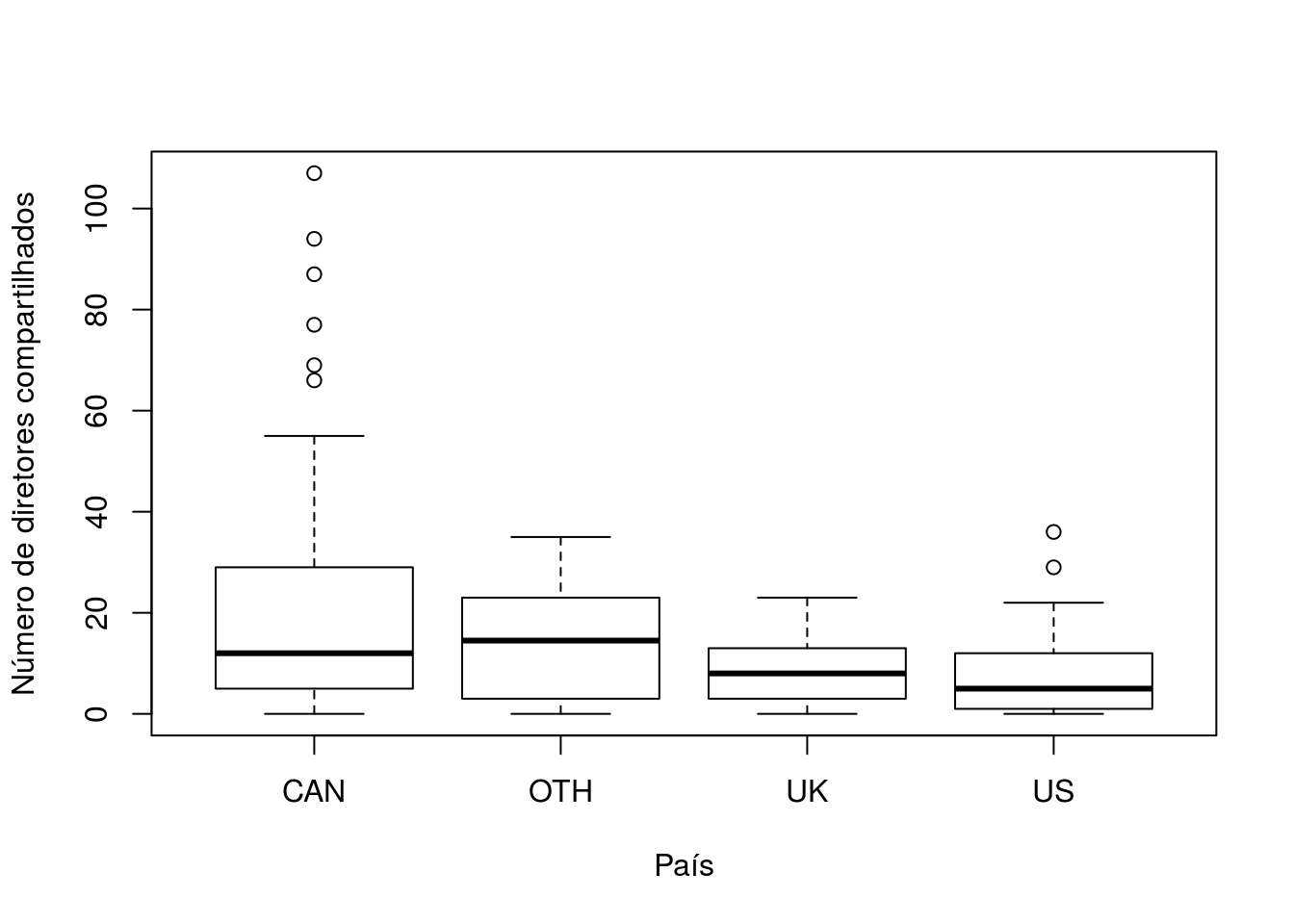
boxplot(Ornstein$interlocks~Ornstein$nation,xlab='País',
        ylab='Número de diretores compartilhados')

boxplot(Ornstein$interlocks~Ornstein$sector,xlab='Setor',
        ylab='Número de diretores compartilhados')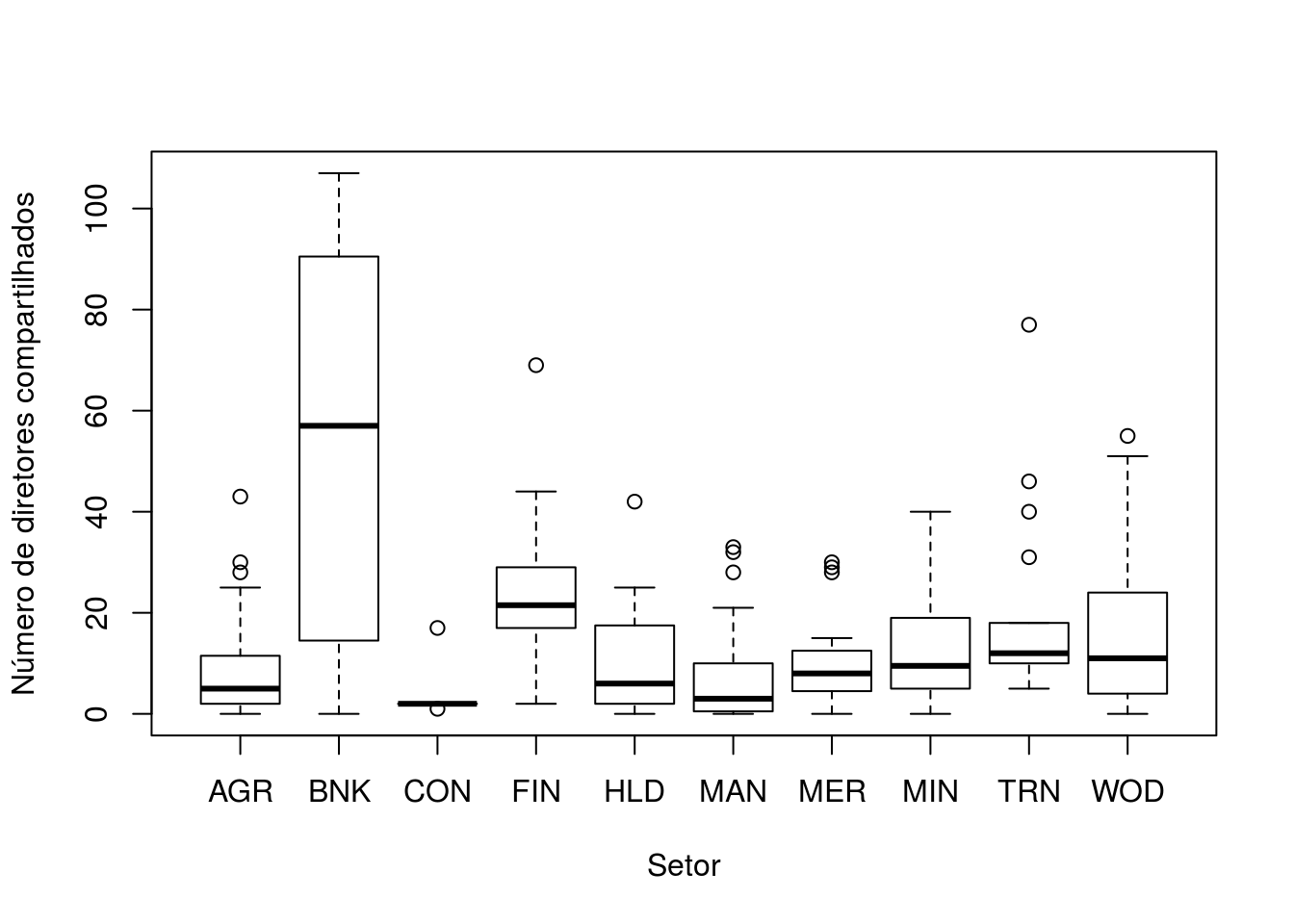

Ajuste 0 - Modelo Normal

Vamos tentar um modelo com erros normais.

ajuste0 <- lm(interlocks ~ log(assets) + nation + sector, data=Ornstein)
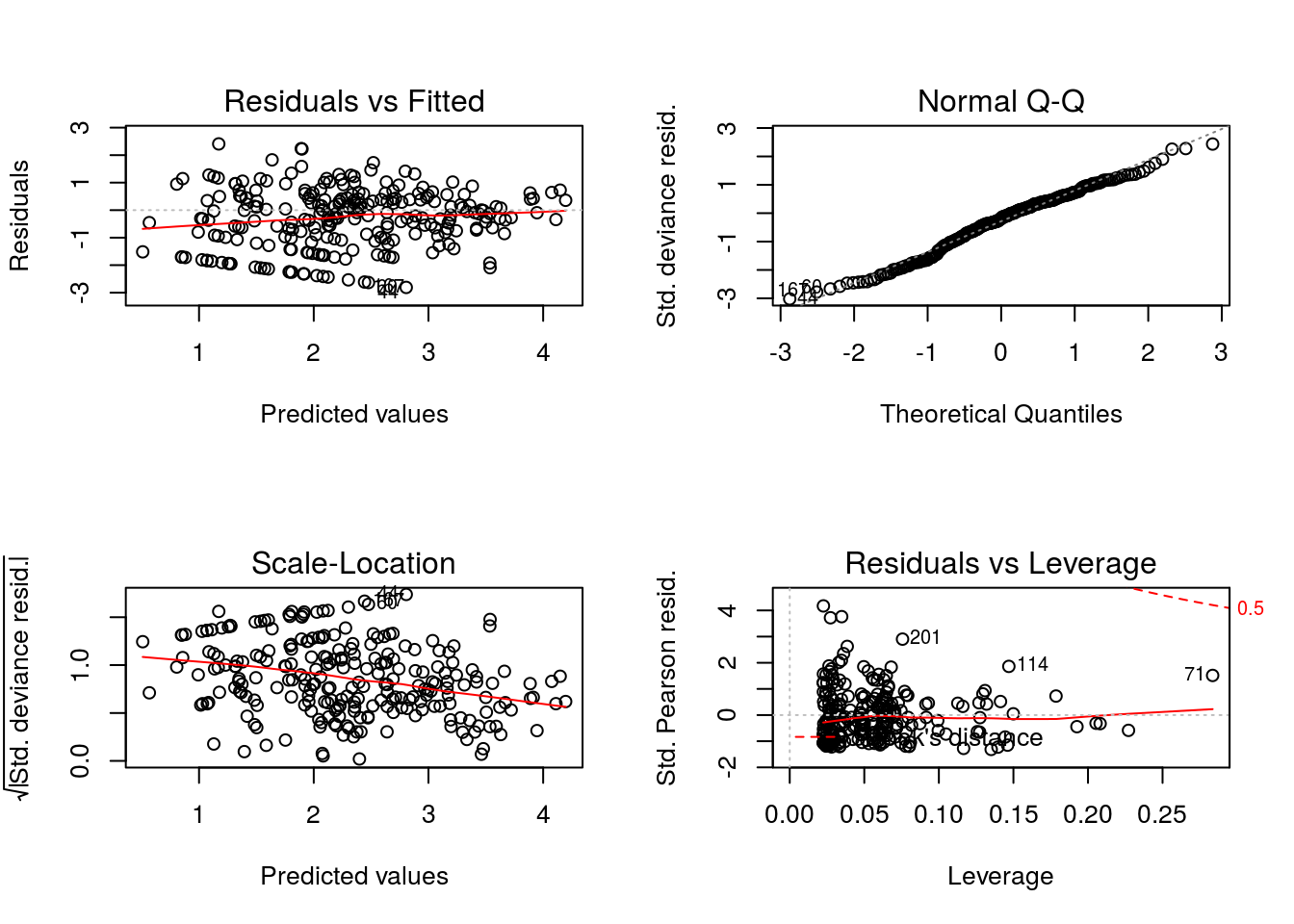
par(mfrow=c(2,2))
plot(ajuste0) # Bah.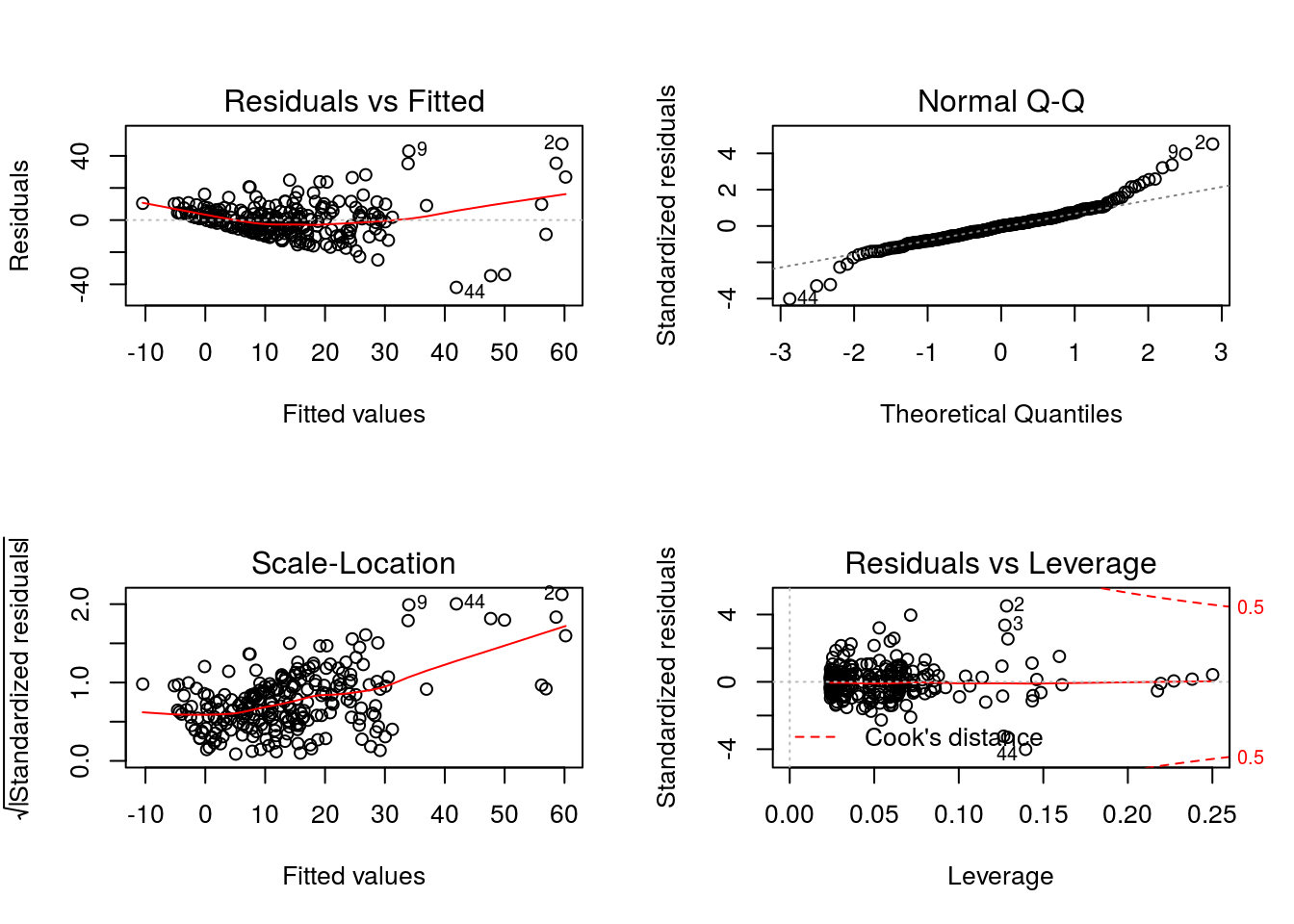

Ajuste 1 - Modelo loglinear Poisson

ajuste1 <- glm(interlocks~log(assets)+nation+sector, family=poisson, data=Ornstein)
summary(ajuste1) 

## 
## Call:
## glm(formula = interlocks ~ log(assets) + nation + sector, family = poisson, 
##     data = Ornstein)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -6.7111  -2.3159  -0.4595   1.2824   6.2849  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.83938    0.13664  -6.143 8.09e-10 ***
## log(assets)  0.45145    0.01698  26.585  < 2e-16 ***
## nationOTH   -0.10699    0.07438  -1.438 0.150301    
## nationUK    -0.38722    0.08951  -4.326 1.52e-05 ***
## nationUS    -0.77239    0.04963 -15.562  < 2e-16 ***
## sectorBNK   -0.16651    0.09575  -1.739 0.082036 .  
## sectorCON   -0.48928    0.21320  -2.295 0.021736 *  
## sectorFIN   -0.11161    0.07571  -1.474 0.140457    
## sectorHLD   -0.01491    0.11924  -0.125 0.900508    
## sectorMAN    0.12187    0.07614   1.600 0.109489    
## sectorMER    0.06157    0.08670   0.710 0.477601    
## sectorMIN    0.24985    0.06888   3.627 0.000286 ***
## sectorTRN    0.15181    0.07893   1.923 0.054453 .  
## sectorWOD    0.49825    0.07560   6.590 4.39e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 3737.0  on 247  degrees of freedom
## Residual deviance: 1547.1  on 234  degrees of freedom
## AIC: 2473.1
## 
## Number of Fisher Scoring iterations: 5

Repare que a deviance residual excede muito o respectivo número de graus de liberdade (1547>>>234). Este é um indicativo de falta de ajuste.

par(mfrow=c(2,2))
plot(ajuste1)

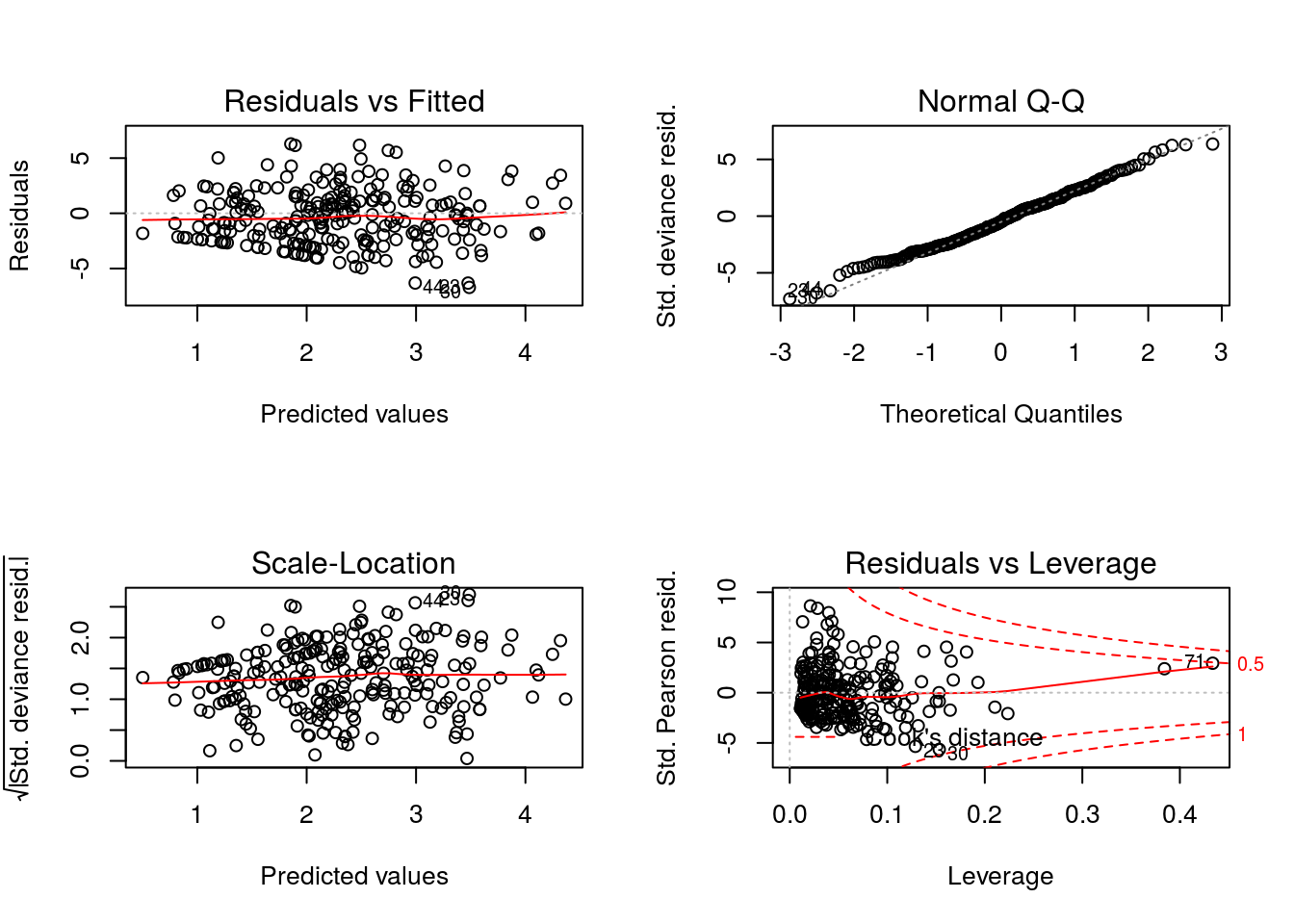
Atentem para a escala dos resíduos, com valores acima de 5 e abaixo de -5!!!

hnp(ajuste1) # Claramente o modelo não se ajusta aos dados.

## Poisson model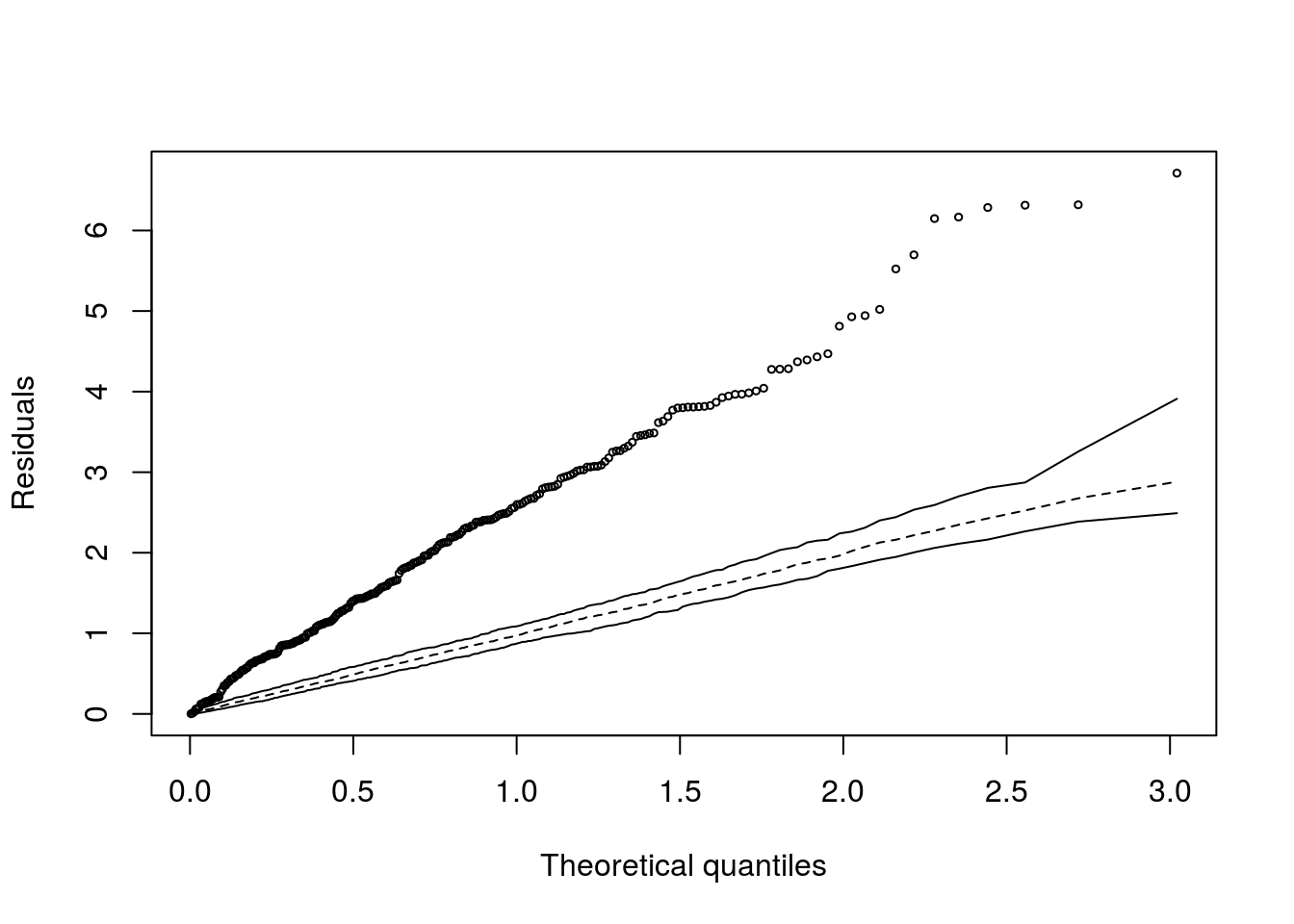

Parâmetro de dispersão

Estimando o parâmetro de dispersão com base na estatística X2 de Pearson:

phi <- sum(rstandard(ajuste1, type='pearson')**2)/234; phi # Muito maior que 1.

## [1] 6.798396

summary(ajuste1, dispersion = phi)

## 
## Call:
## glm(formula = interlocks ~ log(assets) + nation + sector, family = poisson, 
##     data = Ornstein)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -6.7111  -2.3159  -0.4595   1.2824   6.2849  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.83938    0.35626  -2.356   0.0185 *  
## log(assets)  0.45145    0.04428  10.196  < 2e-16 ***
## nationOTH   -0.10699    0.19394  -0.552   0.5812    
## nationUK    -0.38722    0.23338  -1.659   0.0971 .  
## nationUS    -0.77239    0.12941  -5.968  2.4e-09 ***
## sectorBNK   -0.16651    0.24966  -0.667   0.5048    
## sectorCON   -0.48928    0.55589  -0.880   0.3788    
## sectorFIN   -0.11161    0.19741  -0.565   0.5718    
## sectorHLD   -0.01491    0.31091  -0.048   0.9618    
## sectorMAN    0.12187    0.19853   0.614   0.5393    
## sectorMER    0.06157    0.22607   0.272   0.7853    
## sectorMIN    0.24985    0.17960   1.391   0.1642    
## sectorTRN    0.15181    0.20581   0.738   0.4608    
## sectorWOD    0.49825    0.19713   2.528   0.0115 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 6.798396)
## 
##     Null deviance: 3737.0  on 247  degrees of freedom
## Residual deviance: 1547.1  on 234  degrees of freedom
## AIC: 2473.1
## 
## Number of Fisher Scoring iterations: 5

Perceba que os erros padrões estão corrigidos (multiplicados pela \(\sqrt{\phi}\)).

Já corresponde aos resultados de um modelo quase poisson.

sqrt(phi) # Os erros padrões ficam multiplicados por 2.607.

## [1] 2.607373

Ajuste 2 - Modelo Binomial negativa

Como alternativa, vamos ajustar um modelo de regressão com mesma estrutura, mas distribuição binomial negativa.

ajuste2 <- glm.nb(interlocks ~ log(assets) + nation + sector, data=Ornstein)
summary(ajuste2) 

## 
## Call:
## glm.nb(formula = interlocks ~ log(assets) + nation + sector, 
##     data = Ornstein, init.theta = 1.639034209, link = log)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.8087  -0.9897  -0.1886   0.4301   2.4080  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.82535    0.37976  -2.173   0.0298 *  
## log(assets)  0.45618    0.05185   8.799  < 2e-16 ***
## nationOTH   -0.10455    0.23004  -0.454   0.6495    
## nationUK    -0.38945    0.23575  -1.652   0.0985 .  
## nationUS    -0.78820    0.13201  -5.971 2.36e-09 ***
## sectorBNK   -0.40846    0.37726  -1.083   0.2789    
## sectorCON   -0.75698    0.45711  -1.656   0.0977 .  
## sectorFIN   -0.10346    0.25181  -0.411   0.6812    
## sectorHLD   -0.21103    0.34982  -0.603   0.5463    
## sectorMAN    0.07677    0.18601   0.413   0.6798    
## sectorMER    0.07761    0.23246   0.334   0.7385    
## sectorMIN    0.23988    0.18837   1.273   0.2029    
## sectorTRN    0.10133    0.24752   0.409   0.6823    
## sectorWOD    0.39084    0.23253   1.681   0.0928 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(1.639) family taken to be 1)
## 
##     Null deviance: 521.58  on 247  degrees of freedom
## Residual deviance: 296.52  on 234  degrees of freedom
## AIC: 1675.3
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  1.639 
##           Std. Err.:  0.192 
## 
##  2 x log-likelihood:  -1645.257

Repare que o valor da deviance residual, nesse caso, é bem mais próximo do respectivo número de graus de liberdade.

par(mfrow=c(2,2))
plot(ajuste2)

par(mfrow=c(1,1))
hnp(ajuste2)

## Negative binomial model (using MASS package)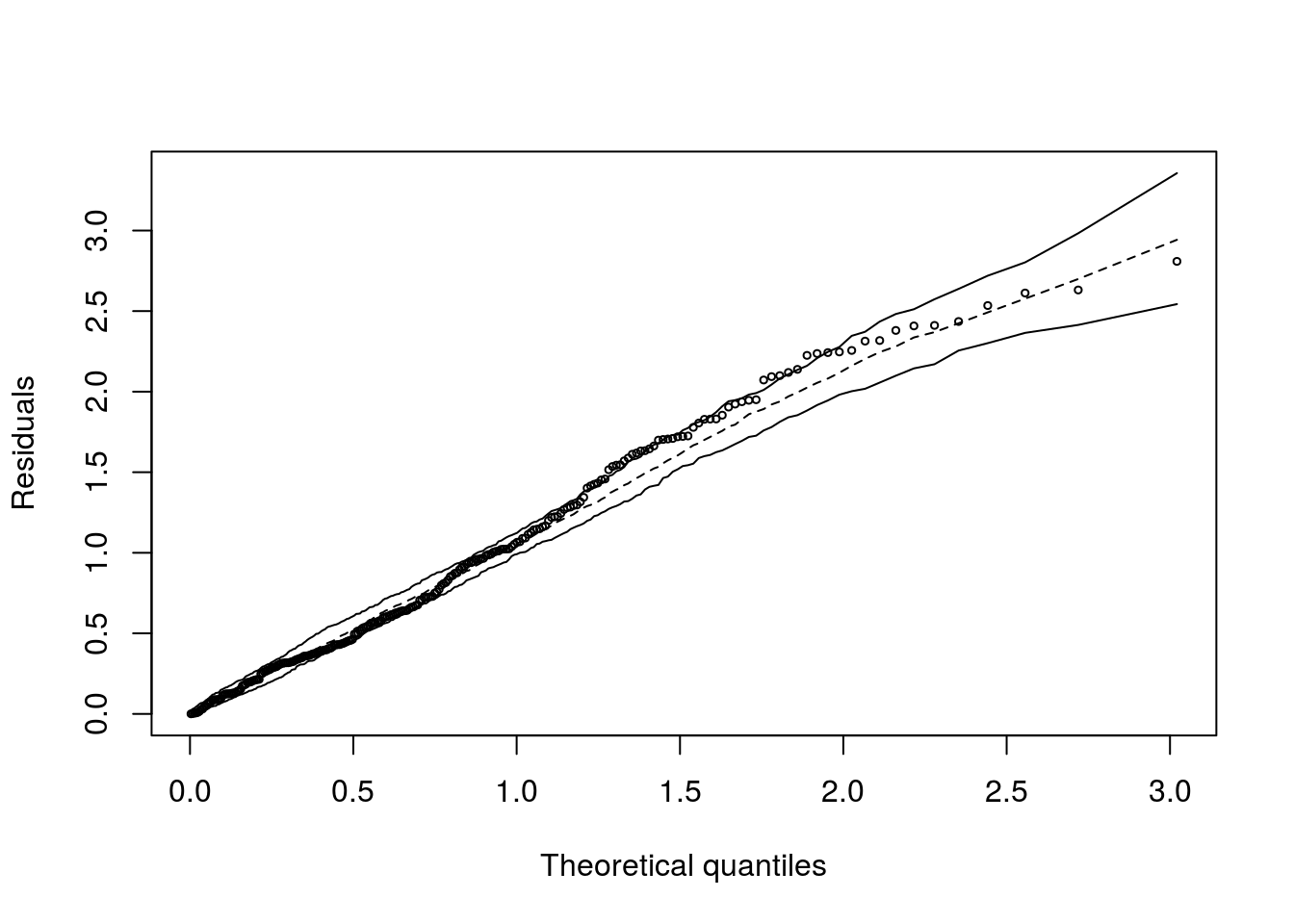

Comparação modelos

Vamos comparar os modelos Poisson e binomial negativa por meio dos AICs:

AIC(ajuste1, ajuste2)

##         df      AIC
## ajuste1 14 2473.102
## ajuste2 15 1675.257

O modelo com melhor ajuste (menor AIC) é o binomial negativo. Vamos seguir com ele.

compareCoefs(ajuste1, ajuste2)

## Calls:
## 1: glm(formula = interlocks ~ log(assets) + nation + sector, family = 
##   poisson, data = Ornstein)
## 2: glm.nb(formula = interlocks ~ log(assets) + nation + sector, data = 
##   Ornstein, init.theta = 1.639034209, link = log)
## 
##             Model 1 Model 2
## (Intercept)  -0.839  -0.825
## SE            0.137   0.380
##                            
## log(assets)  0.4514  0.4562
## SE           0.0170  0.0518
##                            
## nationOTH   -0.1070 -0.1045
## SE           0.0744  0.2300
##                            
## nationUK    -0.3872 -0.3894
## SE           0.0895  0.2357
##                            
## nationUS    -0.7724 -0.7882
## SE           0.0496  0.1320
##                            
## sectorBNK   -0.1665 -0.4085
## SE           0.0958  0.3773
##                            
## sectorCON    -0.489  -0.757
## SE            0.213   0.457
##                            
## sectorFIN   -0.1116 -0.1035
## SE           0.0757  0.2518
##                            
## sectorHLD   -0.0149 -0.2110
## SE           0.1192  0.3498
##                            
## sectorMAN    0.1219  0.0768
## SE           0.0761  0.1860
##                            
## sectorMER    0.0616  0.0776
## SE           0.0867  0.2325
##                            
## sectorMIN    0.2498  0.2399
## SE           0.0689  0.1884
##                            
## sectorTRN    0.1518  0.1013
## SE           0.0789  0.2475
##                            
## sectorWOD    0.4983  0.3908
## SE           0.0756  0.2325
## 

Erros padrões

Observe a diferença dos erros padrões produzidos pelos ajustes dos modelos Poisson e binomial negativo. Os erros produzidos pela Poisson estão subestimados.

confint(ajuste1)

## Waiting for profiling to be done...

##                    2.5 %      97.5 %
## (Intercept) -1.108508434 -0.57287676
## log(assets)  0.418217514  0.48478568
## nationOTH   -0.254554747  0.03710951
## nationUK    -0.566365221 -0.21525523
## nationUS    -0.870179363 -0.67559428
## sectorBNK   -0.354010813  0.02137266
## sectorCON   -0.933489962 -0.09406728
## sectorFIN   -0.259604188  0.03725116
## sectorHLD   -0.254585771  0.21343143
## sectorMAN   -0.027718678  0.27087687
## sectorMER   -0.109959569  0.23012202
## sectorMIN    0.115403223  0.38547023
## sectorTRN   -0.003165433  0.30635642
## sectorWOD    0.349651988  0.64614536

confint(ajuste2)

## Waiting for profiling to be done...

##                   2.5 %      97.5 %
## (Intercept) -1.57345115 -0.07816512
## log(assets)  0.35372210  0.56005140
## nationOTH   -0.55543403  0.37449051
## nationUK    -0.83720228  0.08676612
## nationUS    -1.04218086 -0.53384772
## sectorBNK   -1.16565968  0.39066048
## sectorCON   -1.62097710  0.18292301
## sectorFIN   -0.59221831  0.39460298
## sectorHLD   -0.86401193  0.51798451
## sectorMAN   -0.28770113  0.44182697
## sectorMER   -0.37170403  0.54437543
## sectorMIN   -0.12641357  0.60429312
## sectorTRN   -0.37999614  0.60160690
## sectorWOD   -0.05717997  0.85862294

Os intervalos de confiança baseados na Poisson são excessivamente precisos, comprometendo a taxa de cobertura.

Anova(ajuste2) 

## Analysis of Deviance Table (Type II tests)
## 
## Response: interlocks
##             LR Chisq Df Pr(>Chisq)    
## log(assets)   78.366  1  < 2.2e-16 ***
## nation        38.030  3  2.786e-08 ***
## sector        12.026  9     0.2118    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pelo resultado do teste, o efeito de setor é não significativo (quando o número de diretores é ajustado por país e ativos). Vamos eliminar essa variável do modelo.

Ajuste 3 - Modelo Binomial negativa sem var. “sector”

ajuste3=update(ajuste2, ~.-sector)
summary(ajuste3)

## 
## Call:
## glm.nb(formula = interlocks ~ log(assets) + nation, data = Ornstein, 
##     init.theta = 1.537032922, link = log)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.9616  -1.0596  -0.1868   0.4241   2.1976  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.55007    0.31546  -1.744   0.0812 .  
## log(assets)  0.42611    0.03898  10.930  < 2e-16 ***
## nationOTH   -0.06947    0.21704  -0.320   0.7489    
## nationUK    -0.30001    0.23184  -1.294   0.1957    
## nationUS    -0.72060    0.12395  -5.814 6.11e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(1.537) family taken to be 1)
## 
##     Null deviance: 496.89  on 247  degrees of freedom
## Residual deviance: 295.52  on 243  degrees of freedom
## AIC: 1669
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  1.537 
##           Std. Err.:  0.176 
## 
##  2 x log-likelihood:  -1656.968

O resumo do ajuste indica maior frequência de diretores de empresas norte-americanas em relação às canadenses (referência). Além disso, a frequência (média) de diretores aumenta conforme os ativos da empresa.

Vamos testar a igualdade da frequência média de diretores das empresas que não são norte-americanas.

Ajuste 4 - Modelo Binomial negativa

Ornstein$IndicaUSA <- factor(ifelse(Ornstein$nation=='US','USA','NãoUSA')) 
ajuste4 <- glm.nb(interlocks ~ log(assets)+IndicaUSA,Ornstein)

Agora, vamos testar a restição imposta comparando os modelos 3 e 4.

anova(ajuste3, ajuste4) # A diferença de deviances não é significativa. 

## Likelihood ratio tests of Negative Binomial Models
## 
## Response: interlocks
##                     Model    theta Resid. df    2 x log-lik.   Test    df
## 1 log(assets) + IndicaUSA 1.523329       245       -1658.593             
## 2    log(assets) + nation 1.537033       243       -1656.968 1 vs 2     2
##   LR stat.  Pr(Chi)
## 1                  
## 2 1.625682 0.443596

summary(ajuste4)

## 
## Call:
## glm.nb(formula = interlocks ~ log(assets) + IndicaUSA, data = Ornstein, 
##     init.theta = 1.523329307, link = log)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.9387  -1.0369  -0.1637   0.4179   2.2142  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -0.63978    0.30517  -2.096    0.036 *  
## log(assets)   0.43300    0.03861  11.215  < 2e-16 ***
## IndicaUSAUSA -0.68155    0.11777  -5.787 7.16e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(1.5233) family taken to be 1)
## 
##     Null deviance: 493.53  on 247  degrees of freedom
## Residual deviance: 295.35  on 245  degrees of freedom
## AIC: 1666.6
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  1.523 
##           Std. Err.:  0.174 
## 
##  2 x log-likelihood:  -1658.593

A frequência de diretores compartilhados é inferior nos Estados Unidos em relação às demais localidades estudadas. Estima-se que o número médio de diretores compartilhados nos EUA seja aproximadamente a metade, em relação às demais localidades (exp(-0,68)).

Vamos ajustar um modelo por quasi-verossimilhança, definido pela função de ligação logaritmica e função de variância \(V(\mu)=\phi\mu.\)

Ajuste 6 - Modelo quasi-verossimilhança

ajuste6 <- glm(interlocks ~ log(assets)+IndicaUSA,family=quasi(link='log',variance='mu'),Ornstein)
summary(ajuste6)

## 
## Call:
## glm(formula = interlocks ~ log(assets) + IndicaUSA, family = quasi(link = "log", 
##     variance = "mu"), data = Ornstein)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -6.9034  -2.3786  -0.4741   1.4291   6.8949  
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -0.53533    0.23987  -2.232   0.0265 *  
## log(assets)   0.41849    0.02686  15.581  < 2e-16 ***
## IndicaUSAUSA -0.65209    0.11316  -5.763 2.48e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for quasi family taken to be 6.620681)
## 
##     Null deviance: 3737.0  on 247  degrees of freedom
## Residual deviance: 1659.9  on 245  degrees of freedom
## AIC: NA
## 
## Number of Fisher Scoring iterations: 5

Vamos tentar extrair a logverossimilhança maximizada para esse modelo:

logLik(ajuste6) # Como não especificamos completamente uma distribuição paramétrica, não temos uma verossimilhança.

## 'log Lik.' NA (df=3)

Anova(ajuste6) # Os testes de hipóteses baseiam-se na função quase-desvio 

## Analysis of Deviance Table (Type II tests)
## 
## Response: interlocks
##             LR Chisq Df Pr(>Chisq)    
## log(assets)  231.931  1  < 2.2e-16 ***
## IndicaUSA     36.965  1  1.203e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

e na diferença entre funções quasi-desvio para modelos encaixados que, segundo McCullagh(1983), funciona como o teste da razão de verossimilhanças.

Ajuste 7 - Modelo Poisson

ajuste7 <- glm(interlocks~log(assets)+IndicaUSA,family = poisson,Ornstein)

Modelo de poisson com preditor semelhante aos modelos binomial negativo e de quase-verossimilhança.

Ajuste 8 - Quasi-verossimilhança com função de variância quadrática

ajuste8 <- glm(interlocks ~ log(assets)+IndicaUSA,family=quasi(link='log',variance='mu^2'),Ornstein) 

O ajuste8 também corresponde a um modelo de quase verossimilhança, mas com função de variância quadrática (v(mu) = phi*mu^2).

Vamos comparar os ajustes dos modelos com distribuição de Poisson, binomial nehativa e por quasi verossimilhança.

compareCoefs(ajuste7,ajuste4,ajuste6, ajuste8)

## Calls:
## 1: glm(formula = interlocks ~ log(assets) + IndicaUSA, family = 
##   poisson, data = Ornstein)
## 2: glm.nb(formula = interlocks ~ log(assets) + IndicaUSA, data = 
##   Ornstein, init.theta = 1.523329307, link = log)
## 3: glm(formula = interlocks ~ log(assets) + IndicaUSA, family = 
##   quasi(link = "log", variance = "mu"), data = Ornstein)
## 4: glm(formula = interlocks ~ log(assets) + IndicaUSA, family = 
##   quasi(link = "log", variance = "mu^2"), data = Ornstein)
## 
##              Model 1 Model 2 Model 3 Model 4
## (Intercept)  -0.5353 -0.6398 -0.5353 -0.6764
## SE            0.0932  0.3052  0.2399  0.2977
##                                             
## log(assets)   0.4185  0.4330  0.4185  0.4380
## SE            0.0104  0.0386  0.0269  0.0381
##                                             
## IndicaUSAUSA  -0.652  -0.682  -0.652  -0.689
## SE             0.044   0.118   0.113   0.113
## 

Gráficos de resíduos de Pearson vs valores ajustados para os modelos quasi-poisson (ajuste6) e Poisson (ajuste7). Repare na escala dos resíduos.

par(mfrow=c(1,2),las=1)
plot(fitted(ajuste6),rstudent(ajuste6,type='pearson'),xlab='Preditor ajustado',
     ylab='Resíduo padronizado de Pearson',main='Modelo quasi Poisson')
plot(fitted(ajuste7),rstudent(ajuste7,type='pearson'),xlab='Preditor ajustado',
     ylab='Resíduo padronizado de Pearson',main='Modelo Poisson')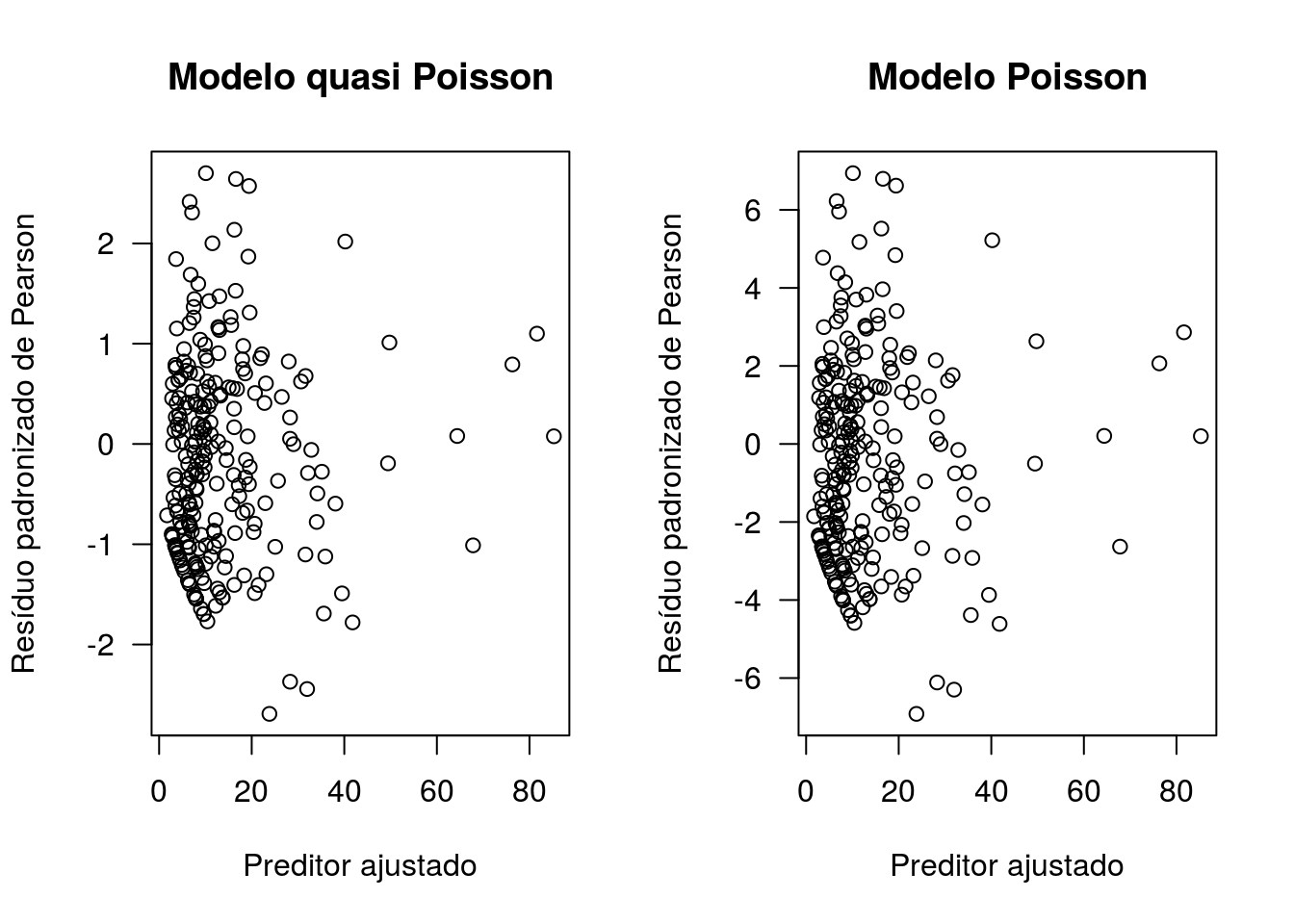

Um pouco mais de diagnóstico:

influenceIndexPlot(ajuste7,vars=c('Studentized','Cook','Hat'),id.n=3)

influenceIndexPlot(ajuste6,vars=c('Studentized','Cook','Hat'),id.n=3)

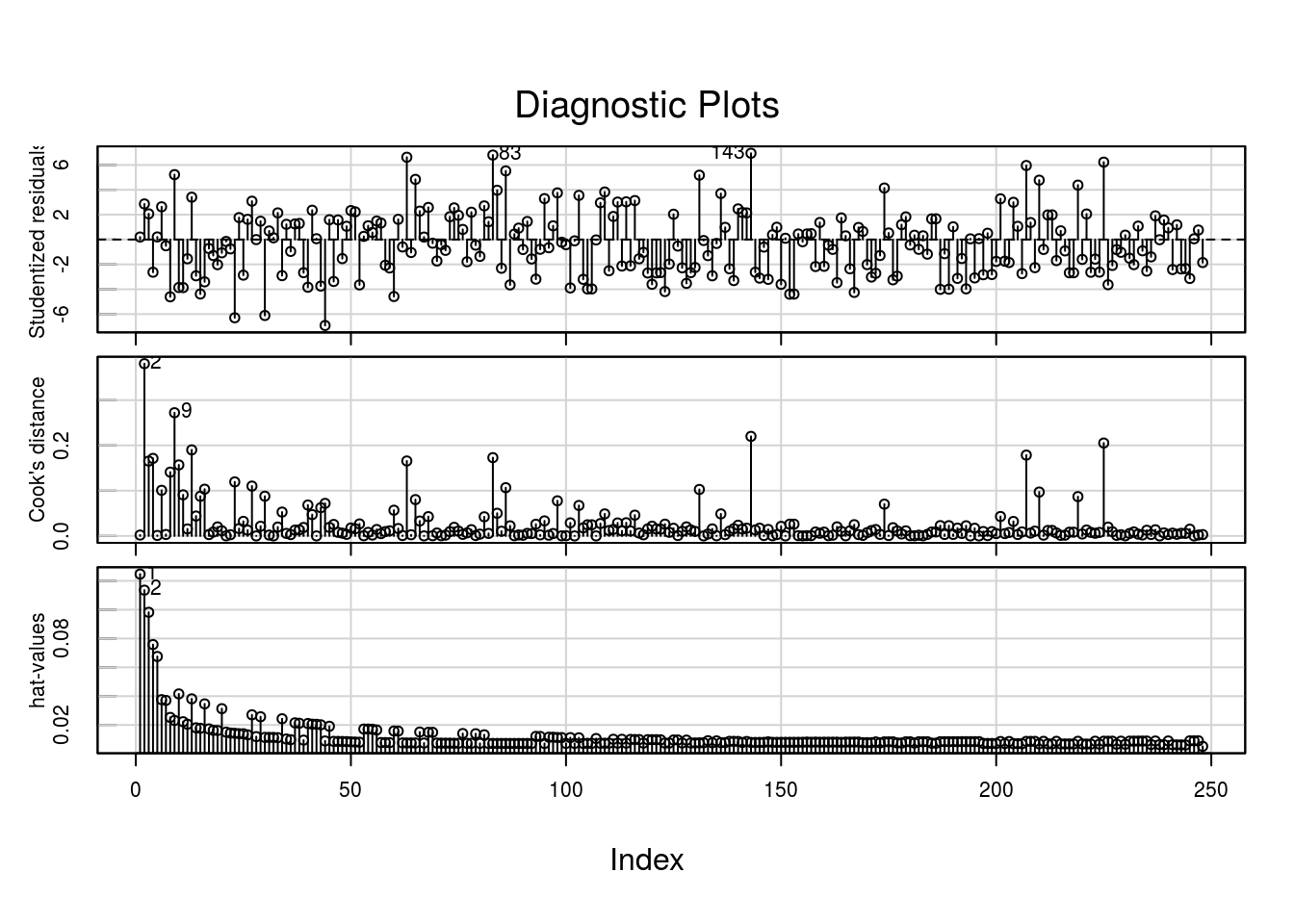
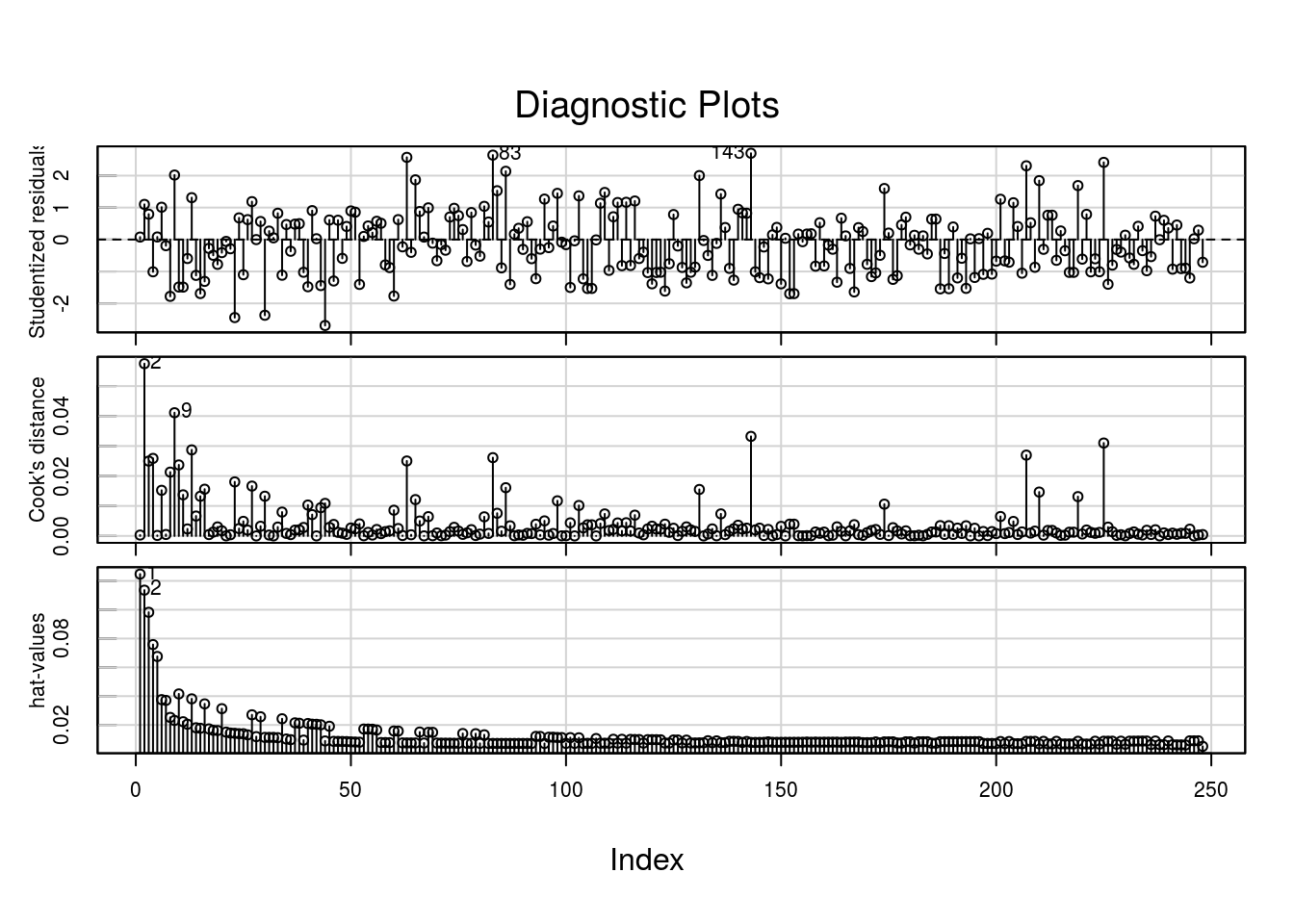
Pode-se observar menor, novamnet, redução na escala dos resíduos e valores consideravelmente menores para as distâncias de Cook para o ajuste6.

Vamos explorar o efeito da quantidade de ativos.

require(effects)
plot(allEffects(ajuste4), type = 'response')

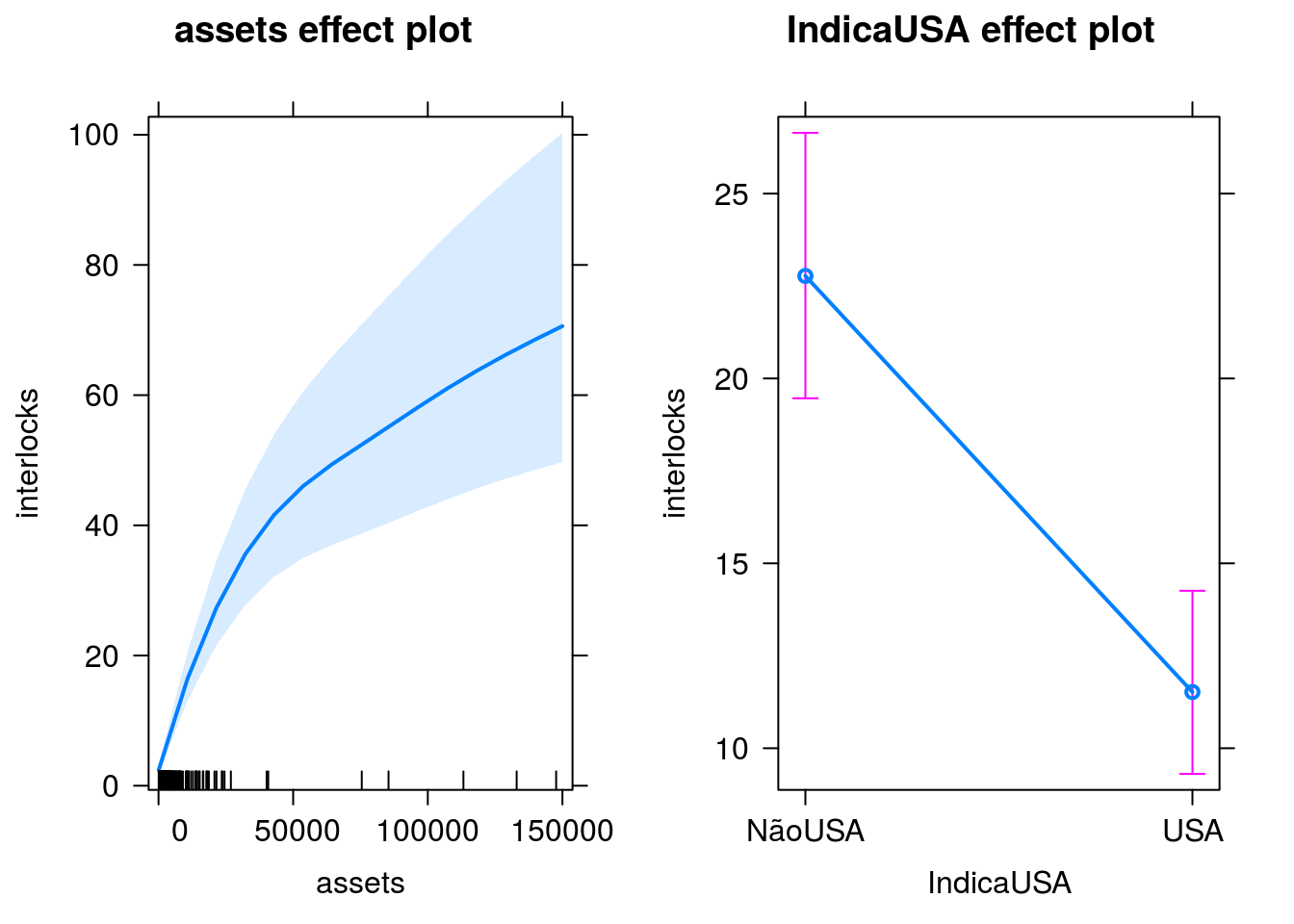
E se usarmos o modelo Poisson com estimação por Bootstrap?

Ajuste Boostrap

ajusteboot <- Boot(ajuste7, R=999)

Observe que usando bootstrap (NÃO PARAMÉTRICO) também contornamos o problema da superdispersão, com erros padrões próximos aos obtidos usando quase verossimilhança e a distribuição binomial negativa.

confint(ajusteboot) # Intervalos de confiança bootstrap.

## Bootstrap bca confidence intervals
## 
##                   2.5 %      97.5 %
## (Intercept)  -0.9722124 -0.02243248
## log(assets)   0.3625008  0.46612668
## IndicaUSAUSA -0.8939350 -0.45466283

confint.default(ajuste6) # Intervalos de confiança baseados no modelo de QL

##                   2.5 %      97.5 %
## (Intercept)  -1.0054652 -0.06519063
## log(assets)   0.3658453  0.47112958
## IndicaUSAUSA -0.8738815 -0.43030087

confint.default(ajuste7) # Intervalos de confiança baseados no MLG Poisson

##                   2.5 %     97.5 %
## (Intercept)  -0.7180426 -0.3526133
## log(assets)   0.3980285  0.4389463
## IndicaUSAUSA -0.7382880 -0.5658944

Os ICs baseados no MLG são incorretamete precisos, em relação aos demais. Ver estudo de simulação em arquivo a parte.

Agora, vamos ajustar o modelo quase poisson com estimação robusta dos erros padrões (estimador sanduíche). Para isso, vamos usar a biblioteca geepack.

Ajuste 9 - Modelo quasi-poisson com estimação robusta dos erros padrões

require(geepack)
Ornstein$Subj <- 1:nrow(Ornstein)
ajuste9 <- geeglm(interlocks ~ log(assets) + IndicaUSA, family = 'poisson', id = Subj, data=Ornstein)
summary(ajuste9)

## 
## Call:
## geeglm(formula = interlocks ~ log(assets) + IndicaUSA, family = "poisson", 
##     data = Ornstein, id = Subj)
## 
##  Coefficients:
##              Estimate  Std.err    Wald Pr(>|W|)    
## (Intercept)  -0.53533  0.23760   5.076   0.0243 *  
## log(assets)   0.41849  0.02567 265.723  < 2e-16 ***
## IndicaUSAUSA -0.65209  0.10561  38.123 6.64e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Estimated Scale Parameters:
##             Estimate Std.err
## (Intercept)    6.541  0.6662
## 
## Correlation: Structure = independenceNumber of clusters:   248   Maximum cluster size: 1