Estimação em modelos lineares generalizados

Ajuste de um GLM: Distribuição de Bernoulli

y <- c(0,0,0,0,1,0,1,1,1,1) # valores para a variável resposta.
x <- 1:10 # valores para a variável explicativa. 

plot(x, y, pch=20)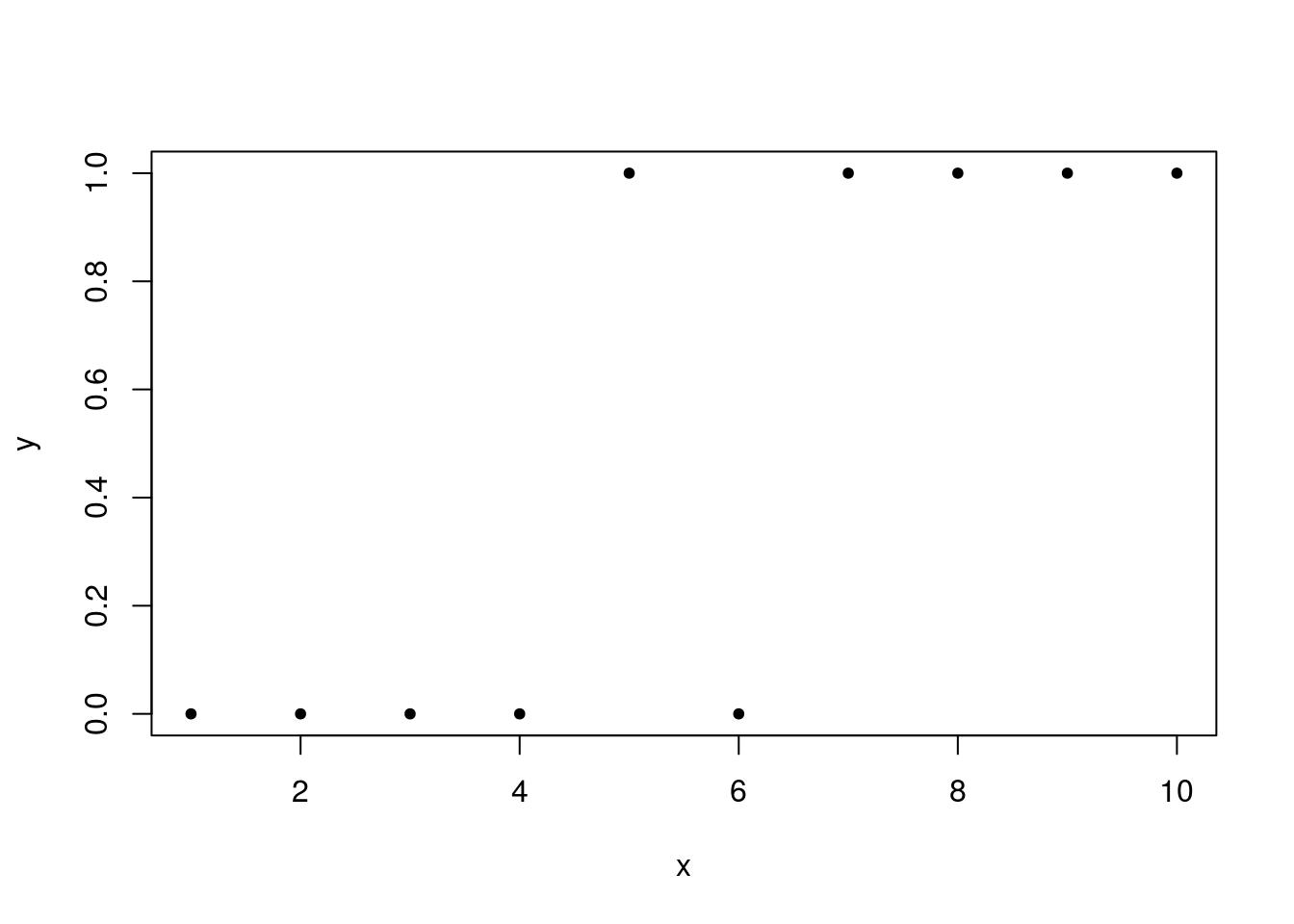

X <- matrix(c(rep(1,10),x),nrow=10) # Matriz do modelo

Matriz do modelo

Passo 1

mu <- c(0.1,0.1,0.1,0.1,0.9,0.1,0.9,0.9,0.9,0.9) 
# Chute inicial

z <- log(mu/(1-mu)) + (y-mu)/(mu*(1-mu))
z

##  [1] -3.308336 -3.308336 -3.308336 -3.308336  3.308336 -3.308336  3.308336
##  [8]  3.308336  3.308336  3.308336

# Variável dependente ajustada

w <- (mu*(1-mu))
w

##  [1] 0.09 0.09 0.09 0.09 0.09 0.09 0.09 0.09 0.09 0.09

Pesos

beta <- lm(z ~ x, weights = w)$coefficients
beta

## (Intercept)           x 
##  -5.0727814   0.9223239

# betas para o próximo passo.

eta <- X %*% beta
eta

##             [,1]
##  [1,] -4.1504575
##  [2,] -3.2281336
##  [3,] -2.3058097
##  [4,] -1.3834858
##  [5,] -0.4611619
##  [6,]  0.4611619
##  [7,]  1.3834858
##  [8,]  2.3058097
##  [9,]  3.2281336
## [10,]  4.1504575

# preditor linear para o próximo passo.

mu <- exp(eta)/(exp(eta)+1)
mu

##             [,1]
##  [1,] 0.01551277
##  [2,] 0.03812062
##  [3,] 0.09064294
##  [4,] 0.20044974
##  [5,] 0.38671021
##  [6,] 0.61328979
##  [7,] 0.79955026
##  [8,] 0.90935706
##  [9,] 0.96187938
## [10,] 0.98448723

mu para o próximo passo.

Passo 2

Atualizamos os valores de z e w com os resultados do passo 1

z <- log(mu/(1-mu)) + (y-mu)/(mu*(1-mu))
z

##            [,1]
##  [1,] -5.166215
##  [2,] -4.267765
##  [3,] -3.405488
##  [4,] -2.634189
##  [5,]  2.124754
##  [6,] -2.124754
##  [7,]  2.634189
##  [8,]  3.405488
##  [9,]  4.267765
## [10,]  5.166215

Variável dependente ajustada

w <- (mu*(1-mu))
w

##             [,1]
##  [1,] 0.01527212
##  [2,] 0.03666744
##  [3,] 0.08242680
##  [4,] 0.16026964
##  [5,] 0.23716542
##  [6,] 0.23716542
##  [7,] 0.16026964
##  [8,] 0.08242680
##  [9,] 0.03666744
## [10,] 0.01527212

Pesos

beta <- lm(z ~ x, weights = w)$coefficients
beta

## (Intercept)           x 
##   -6.449377    1.172614

betas para o próximo passo.

eta <- X %*% beta
eta

##            [,1]
##  [1,] -5.276763
##  [2,] -4.104149
##  [3,] -2.931535
##  [4,] -1.758921
##  [5,] -0.586307
##  [6,]  0.586307
##  [7,]  1.758921
##  [8,]  2.931535
##  [9,]  4.104149
## [10,]  5.276763

preditor linear para o próximo passo.

mu <- exp(eta)/(exp(eta)+1)
mu

##              [,1]
##  [1,] 0.005082975
##  [2,] 0.016236101
##  [3,] 0.050616520
##  [4,] 0.146925543
##  [5,] 0.357482657
##  [6,] 0.642517343
##  [7,] 0.853074457
##  [8,] 0.949383480
##  [9,] 0.983763899
## [10,] 0.994917025

Mu para o próximo passo

Passo 3

Atualizamos os valores de z e w com os resultados do passo 2

z <- log(mu/(1-mu)) + (y-mu)/(mu*(1-mu))
z

##            [,1]
##  [1,] -6.281872
##  [2,] -5.120653
##  [3,] -3.984850
##  [4,] -2.931152
##  [5,]  2.211032
##  [6,] -2.211032
##  [7,]  2.931152
##  [8,]  3.984850
##  [9,]  5.120653
## [10,]  6.281872

Variável dependente ajustada

w <- (mu*(1-mu))
w

##              [,1]
##  [1,] 0.005057138
##  [2,] 0.015972490
##  [3,] 0.048054488
##  [4,] 0.125338428
##  [5,] 0.229688807
##  [6,] 0.229688807
##  [7,] 0.125338428
##  [8,] 0.048054488
##  [9,] 0.015972490
## [10,] 0.005057138

Pesos

beta <- lm(z ~ x, weights = w)$coefficients
beta

## (Intercept)           x 
##   -7.067324    1.284968

betas para o próximo passo.

eta <- X %*% beta
eta

##            [,1]
##  [1,] -5.782356
##  [2,] -4.497388
##  [3,] -3.212420
##  [4,] -1.927452
##  [5,] -0.642484
##  [6,]  0.642484
##  [7,]  1.927452
##  [8,]  3.212420
##  [9,]  4.497388
## [10,]  5.782356

preditor linear para o próximo passo.

mu <- exp(eta)/(exp(eta)+1)
mu

##             [,1]
##  [1,] 0.00307198
##  [2,] 0.01101536
##  [3,] 0.03870100
##  [4,] 0.12703286
##  [5,] 0.34468524
##  [6,] 0.65531476
##  [7,] 0.87296714
##  [8,] 0.96129900
##  [9,] 0.98898464
## [10,] 0.99692802

mu para o próximo passo.

Passo 4

Atualizamos os valores de z e w com os resultados do passo 3

z <- log(mu/(1-mu)) + (y-mu)/(mu*(1-mu))
z

##            [,1]
##  [1,] -6.785438
##  [2,] -5.508526
##  [3,] -4.252679
##  [4,] -3.072971
##  [5,]  2.258714
##  [6,] -2.258714
##  [7,]  3.072971
##  [8,]  4.252679
##  [9,]  5.508526
## [10,]  6.785438

Variável dependente ajustada

w <- (mu*(1-mu))
w

##              [,1]
##  [1,] 0.003062543
##  [2,] 0.010894021
##  [3,] 0.037203229
##  [4,] 0.110895515
##  [5,] 0.225877324
##  [6,] 0.225877324
##  [7,] 0.110895515
##  [8,] 0.037203229
##  [9,] 0.010894021
## [10,] 0.003062543

Pesos

beta <- lm(z ~ x, weights = w)$coefficients
beta

## (Intercept)           x 
##   -7.157411    1.301348

betas para o próximo passo.

eta <- X %*% beta
eta

##             [,1]
##  [1,] -5.8560638
##  [2,] -4.5547163
##  [3,] -3.2533688
##  [4,] -1.9520213
##  [5,] -0.6506738
##  [6,]  0.6506738
##  [7,]  1.9520213
##  [8,]  3.2533688
##  [9,]  4.5547163
## [10,]  5.8560638

preditor linear para o próximo passo.

mu <- exp(eta)/(exp(eta)+1)
mu

##              [,1]
##  [1,] 0.002854318
##  [2,] 0.010408017
##  [3,] 0.037206023
##  [4,] 0.124333126
##  [5,] 0.342837724
##  [6,] 0.657162276
##  [7,] 0.875666874
##  [8,] 0.962793977
##  [9,] 0.989591983
## [10,] 0.997145682

mu para o próximo passo. Agora repetimos esse passo atualizando o valor de mu.

Repetição

Agora, vamos repetir o processo para 10 passos

beta <- matrix(0, nrow=10, ncol=2)

Matriz que vai armazenar as estimativas.

epsilon <- numeric()

Vetor que vai armazenar as diferenças entre os resultados de simulações sucessivas.

for(i in 1:10){
  if(i==1) {mu <- c(0.1,0.1,0.1,0.1,0.9,0.1,0.9,0.9,0.9,0.9) 
  # Se for a primeira iteração, então usamos nossos chutes iniciais.
  eta <- log(mu/(1-mu))}
  
  if (i!=1) {
    eta <- X %*% beta[i-1,] 
    mu <- exp(eta)/(exp(eta)+1) 
  }
  z <- log(mu/(1-mu)) + (y-mu)/(mu*(1-mu))
  w <- (mu*(1-mu))
  beta[i,] <- lm(z ~ x, weights = w)$coefficients
  if(i>1) epsilon[i-1] <- sum(((beta[i,]-beta[i-1,])/beta[i-1,])**2)
}

Próximo passo

Agora, vamos ajustar o modelo declarando a log-verossimilhança a um otimizador do R.

require(bbmle)

## Loading required package: bbmle

## Loading required package: stats4

logvero <- function(b0, b1)
  -sum(dbinom(y, 1, exp(b0 + b1 * x)/ (1+exp(b0 + b1 * x)), log=T))

logvero armazena a função de log verossimilhança (-)

Precisamos de valores iniciais para beta0 e beta1. Vamos chutar valores iniciais para mu e fazer uma regressão linear simples de ln(mu/(1-mu)) ~ x

mu <- c(0.1,0.1,0.1,0.1,0.9,0.1,0.9,0.9,0.9,0.9)
ajuste <- lm(log((mu)/(1-mu)) ~ x) 
# Regressando g(mu) em função de x para obter valores iniciais para b0 e b1.

est2 <- mle2(logvero,start=list(b0=-3.23, b1=0.13))
est2

## 
## Call:
## mle2(minuslogl = logvero, start = list(b0 = -3.23, b1 = 0.13))
## 
## Coefficients:
##        b0        b1 
## -7.159287  1.301686 
## 
## Log-likelihood: -2.51

Gráfico

logvero2 <- function(b0, b1,data){
  l <- sum(dbinom(data$y, 1, exp(b0 + b1 * data$x)/ (1+exp(b0 + b1 * data$x)), log=T))
  return(l)
}

data <- data.frame(x,y)
f <- Vectorize(logvero2,vectorize.args=c("b0","b1"))
b0 <- seq(-15, 0, length.out = 50)
b1 <- seq(0.5, 2.5, length.out = 50)
z <- outer(b0, b1, FUN = f, data)
zlim    <- range(z[!is.na(z)])
palette <- rev(rainbow(20))
colors  <- palette[19*(z-zlim[1])/diff(zlim) + 1] 
require(rgl)

## Loading required package: rgl

persp3d(b0, b1, z, col=colors)

Finalmente, usemos a função glm.

ajuste <- glm(y ~ x, family = binomial(link = "logit"))
names(ajuste)

##  [1] "coefficients"      "residuals"         "fitted.values"    
##  [4] "effects"           "R"                 "rank"             
##  [7] "qr"                "family"            "linear.predictors"
## [10] "deviance"          "aic"               "null.deviance"    
## [13] "iter"              "weights"           "prior.weights"    
## [16] "df.residual"       "df.null"           "y"                
## [19] "converged"         "boundary"          "model"            
## [22] "call"              "formula"           "terms"            
## [25] "data"              "offset"            "control"          
## [28] "method"            "contrasts"         "xlevels"

coef(ajuste) 

## (Intercept)           x 
##   -7.159011    1.301638

Estimativas dos coeficientes do modelo.

fitted(ajuste) 

##           1           2           3           4           5           6 
## 0.002850596 0.010397540 0.037179991 0.124285645 0.342804967 0.657195033 
##           7           8           9          10 
## 0.875714355 0.962820009 0.989602460 0.997149404

Probabilidades ajustadas pelo modelo para cada valor de x na amostra.

predict(ajuste, newdata = data.frame(x = c(3.5, 5.5, 7.5))) 

##         1         2         3 
## -2.603277  0.000000  2.603277

Estimativas (na escala do preditor) para x=3.5; x=5.5 e x=7.5.

predict(ajuste, newdata = data.frame(x = c(3.5, 5.5, 7.5)),type='response') 

##          1          2          3 
## 0.06892784 0.50000000 0.93107216

Estimativas (na escala da resposta - probabilidades estimadas) para x=3.5; x=5.5 e x=7.5.

summary(ajuste) 

## 
## Call:
## glm(formula = y ~ x, family = binomial(link = "logit"))
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.4633  -0.2426   0.0000   0.2426   1.4633  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)
## (Intercept)   -7.159      4.759  -1.504    0.133
## x              1.302      0.840   1.550    0.121
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 13.863  on 9  degrees of freedom
## Residual deviance:  5.018  on 8  degrees of freedom
## AIC: 9.018
## 
## Number of Fisher Scoring iterations: 6

Resumo do modelo ajustado contendo, dentre outras coisas, as estimativas dos betas e os correspondnetes erros padrões.

vcov(ajuste)

##             (Intercept)          x
## (Intercept)   22.648750 -3.8806414
## x             -3.880641  0.7055712

Matriz de variâncias e covariâncias estimada para \(\hat{\beta}\)

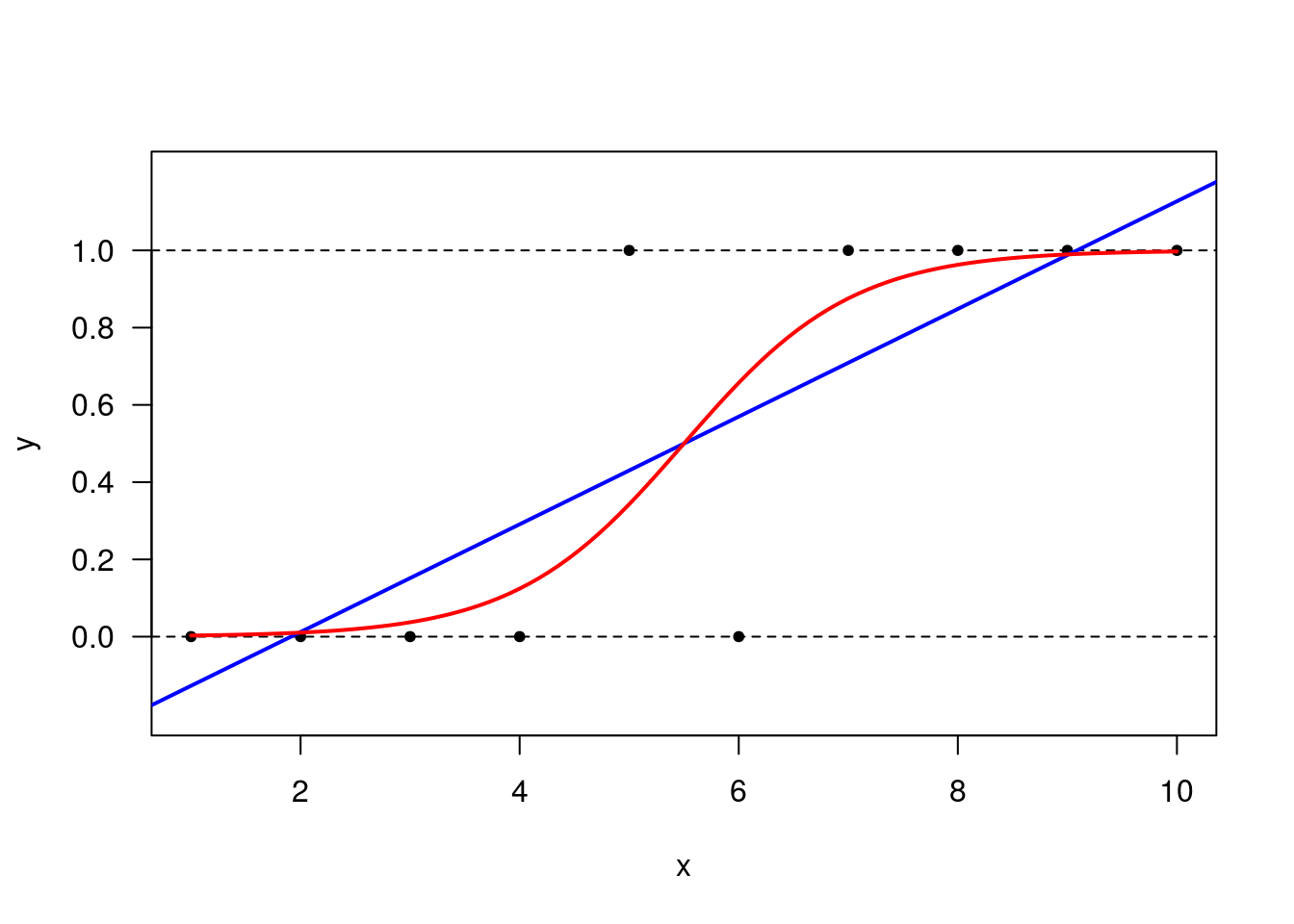
Vamos acrescentar ao gráfico o modelo ajustado. Antes, começamos tentando o ajuste de um modelo linear.

plot(x, y, pch=20, ylim = c(-0.2, 1.2), yaxt = 'n')
axis(2, seq(0, 1, 0.2), las = 1)
abline(h = 0, lty = 2)
abline(h = 1, lty = 2)

ajuste_lin <- lm(y ~ x)
abline(coefficients(ajuste_lin), col='blue', lwd = 2)

# Agora para o glm:

x.grid <- seq(1, 10, length.out = 100)
lines(x.grid, predict(ajuste, newdata = data.frame(x = x.grid), 
                      type = 'response'), col = 'red', lwd = 2)