Tempo de vida de turbinas de avião

Resultados de um experimento conduzido para avaliar o desempenho de cinco tipos de turb de alta velocidade para motores de avião. Foram considerados dez motores para cada de turb e registrado o tempo (em unidades de milhões de ciclos) até a perda da velocidade.

require(devtools)
require(labestData)
require(MASS)
require(hnp)
data(PaulaTb2.1)
help(PaulaTb2.1)

Análise descritiva

with(PaulaTb2.1, boxplot(tempo ~ turb, xlab='Tipo de turbina', 
                       ylab='tempo até perda de velocidade (milhões de ciclos)'))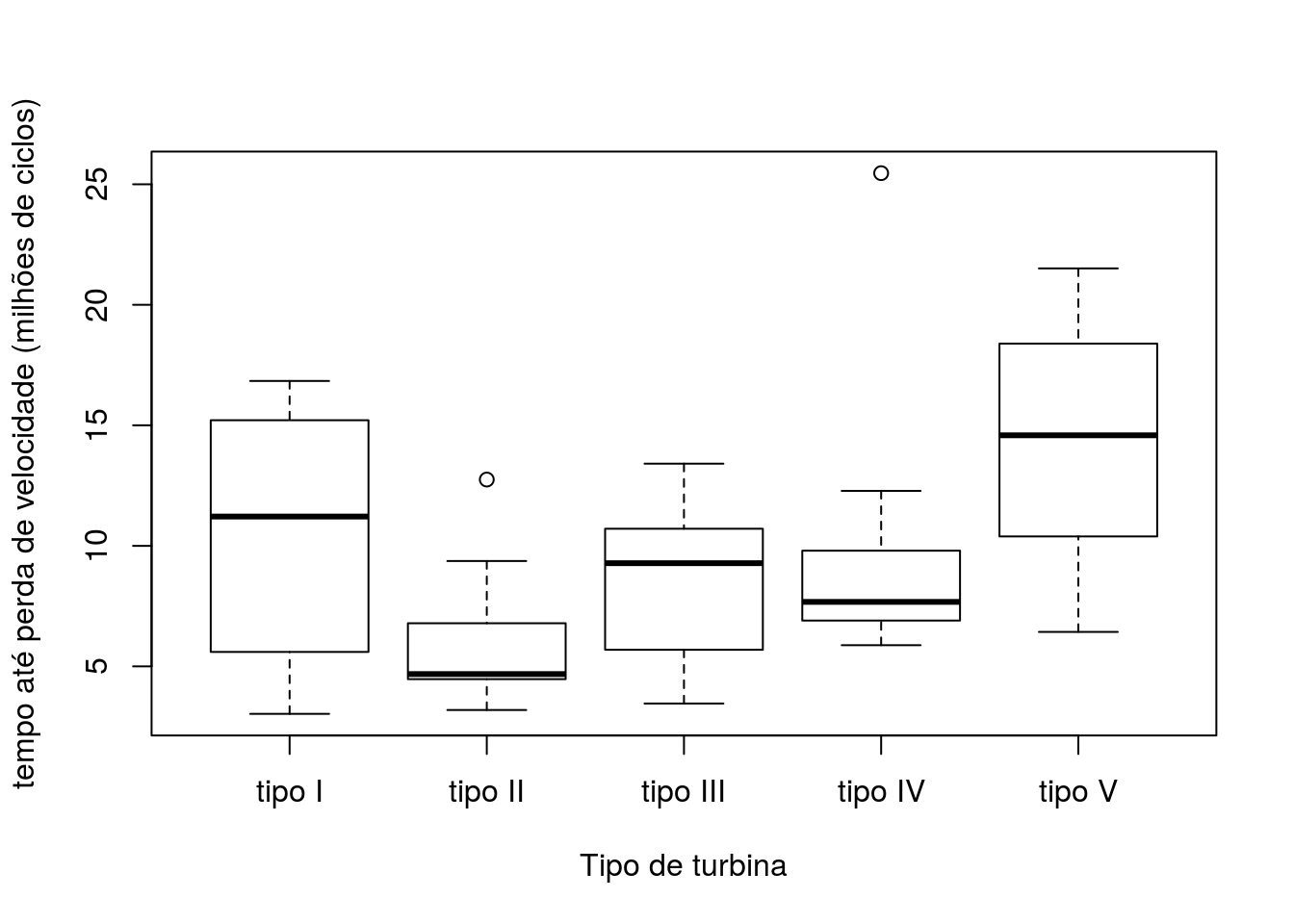

medias <- with(PaulaTb2.1, tapply(tempo,turb,mean)); medias

##   tipo I  tipo II tipo III  tipo IV   tipo V 
##   10.693    6.050    8.636    9.798   14.706

variancias <- with(PaulaTb2.1, tapply(tempo,turb,var)); variancias

##   tipo I  tipo II tipo III  tipo IV   tipo V 
##   23.226    8.497   10.828   33.712   23.652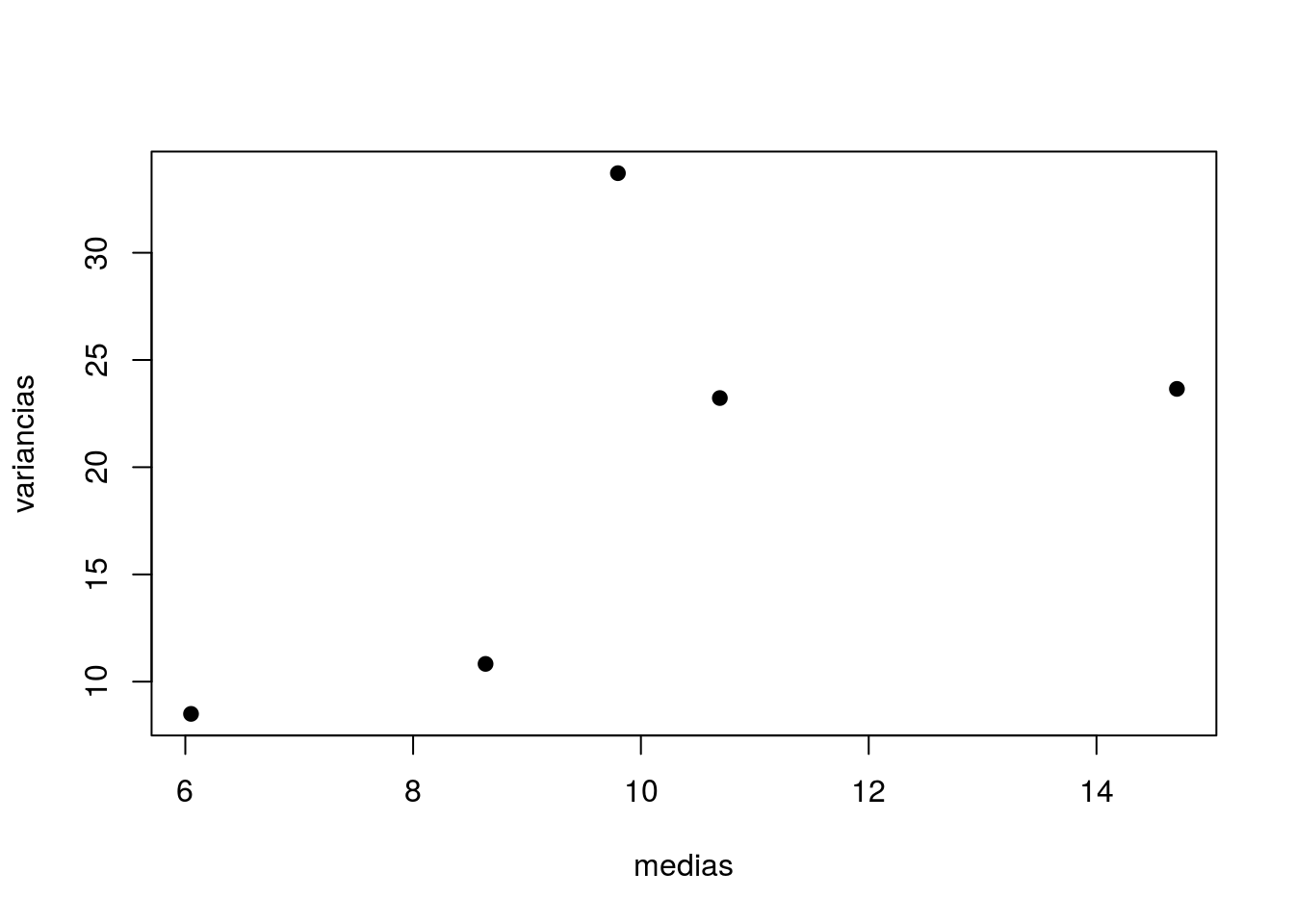

plot(medias, variancias, pch=20, cex=1.5)

cvs <- sqrt(variancias)/medias; cvs # Coeficientes de variação.

##   tipo I  tipo II tipo III  tipo IV   tipo V 
##   0.4507   0.4818   0.3810   0.5926   0.3307

Ajuste 0: modelo normal (com ligação identidade)

ajuste0 <- glm(tempo ~ turb, data = PaulaTb2.1)
par(mfrow = c(2,2))
plot(ajuste0)

par(mfrow = c(1,1))
hnp(ajuste0)

## Gaussian model (glm object)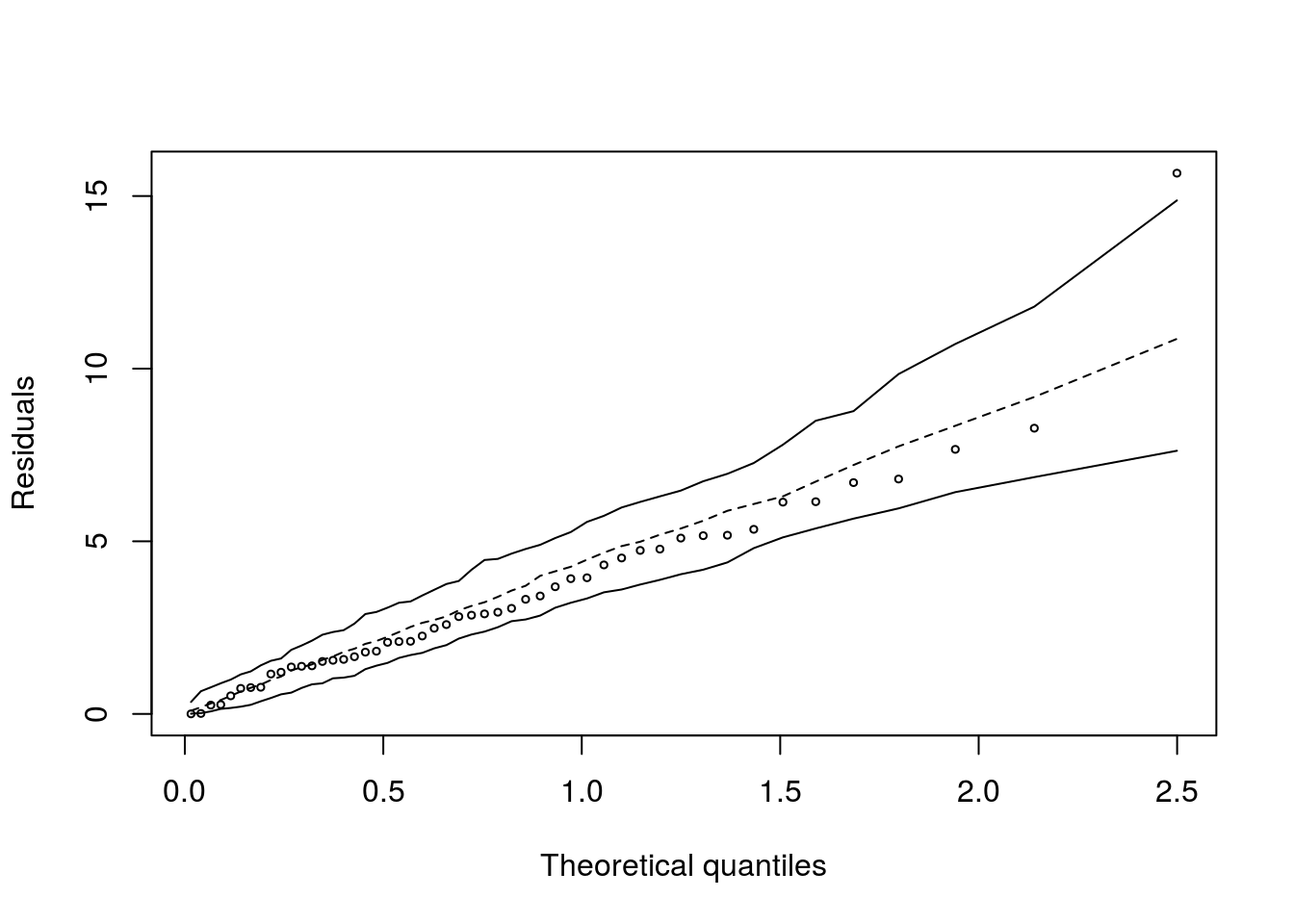

AIC(ajuste0)

## [1] 298.4

Ajuste 1: modelo gamma (com ligação identidade, para comparação)

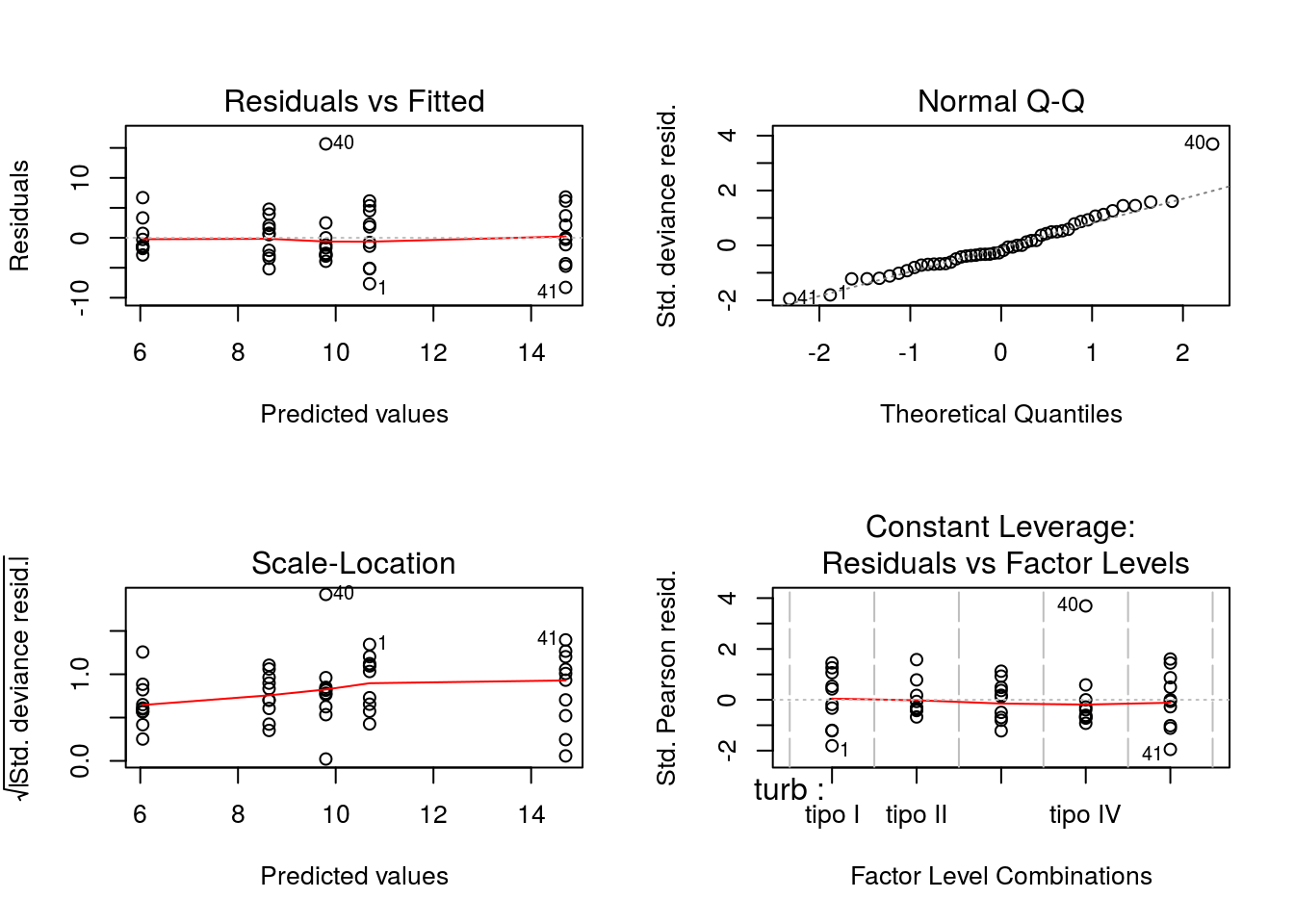
ajuste1 <- glm(tempo ~ turb, family = 'Gamma'(link = 'identity'), data = PaulaTb2.1)

par(mfrow = c(2,2))
plot(ajuste1)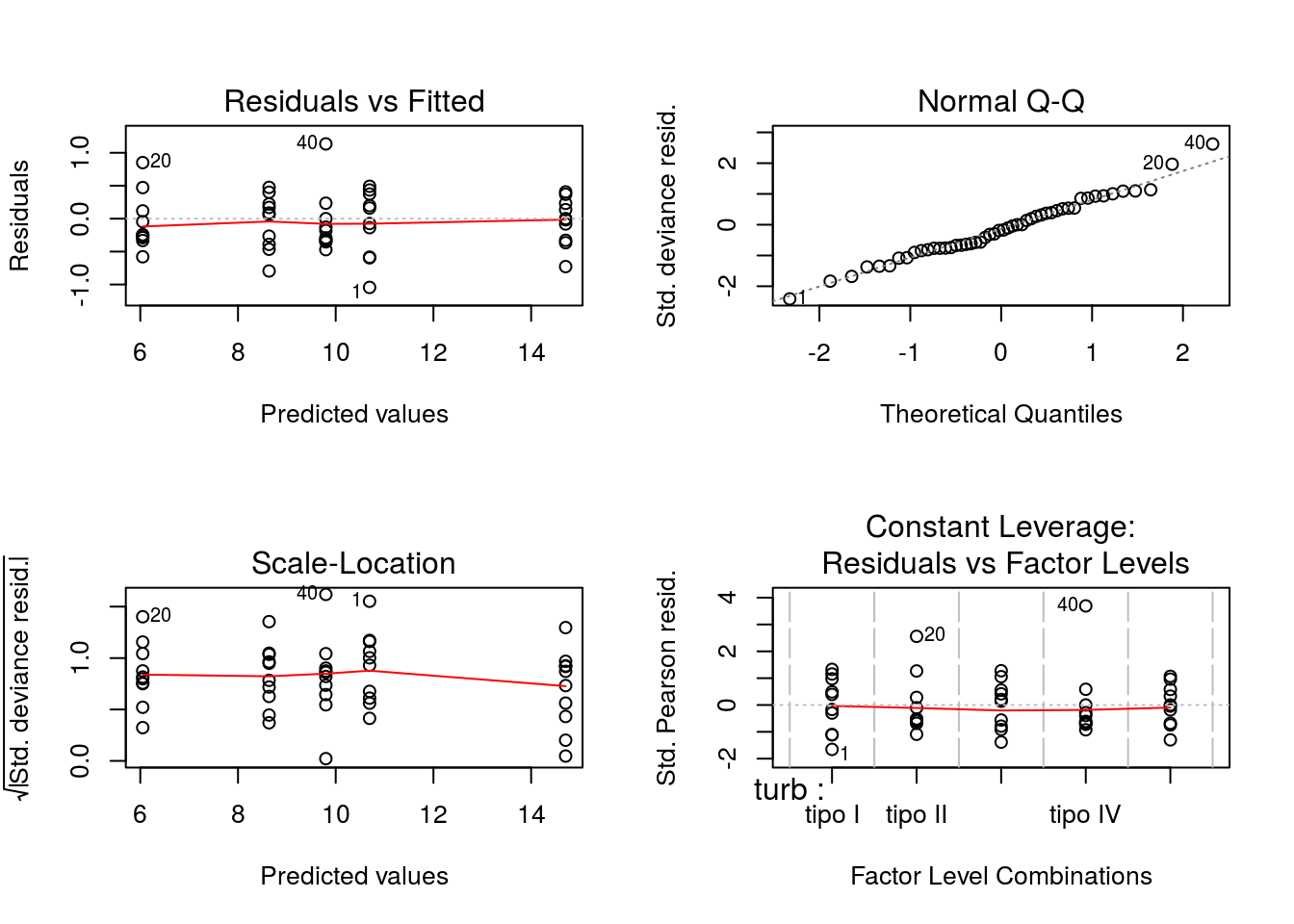

par(mfrow = c(1,1))
hnp(ajuste1)

## Gamma model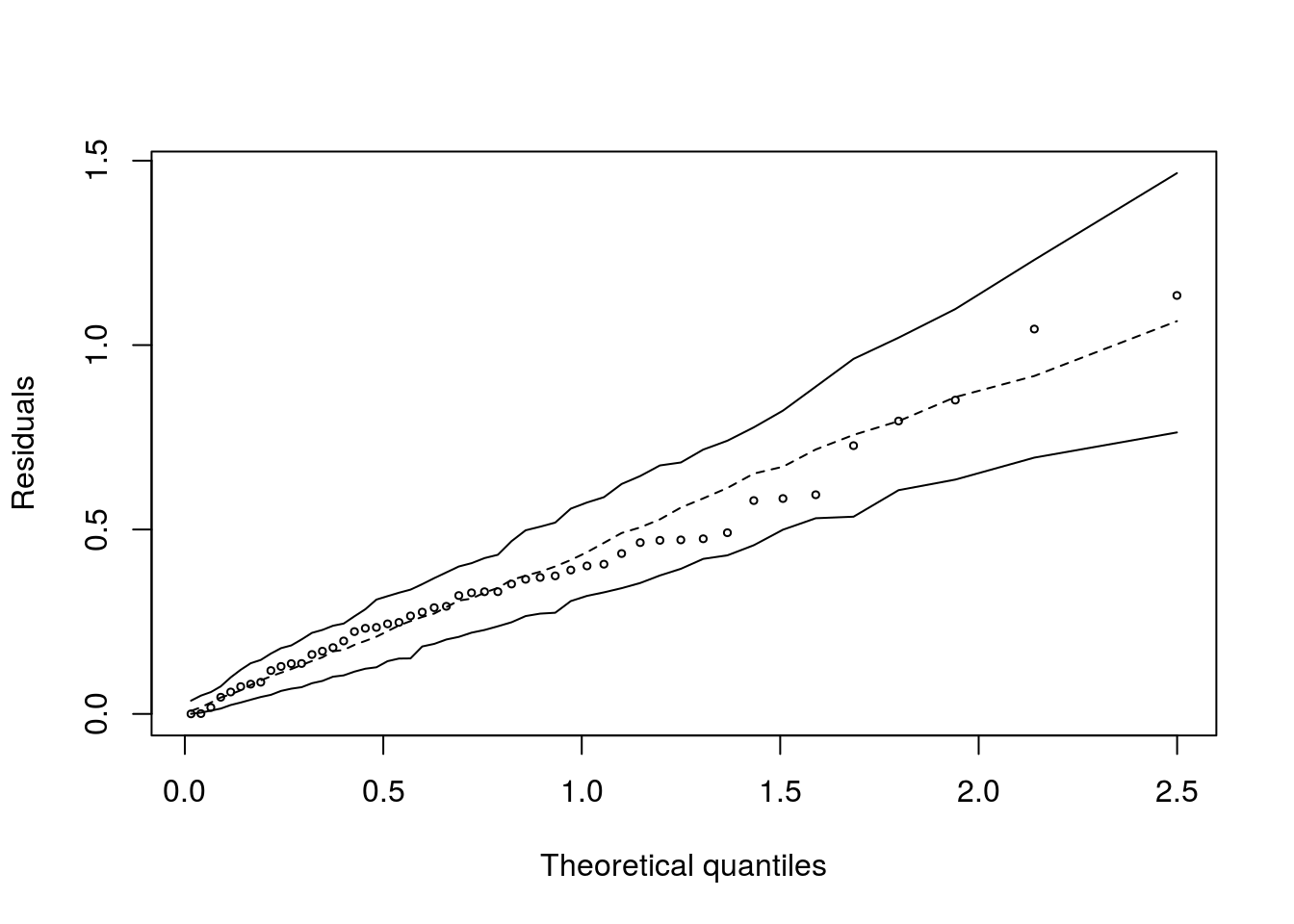

AIC(ajuste1)

## [1] 285.9

Vamos estimar o parâmetro de dispersão.

estimat1 <- ajuste1$deviance/ajuste1$df.residual ; estimat1 

## [1] 0.1969

Baseado na deviance.

estimat2 <- sum(residuals(ajuste1,type='pearson')**2)/ajuste1$df.residual ; estimat2 

## [1] 0.2082

Baseada na estatística X2 de Pearson.

estimat3 <- gamma.dispersion(ajuste1) 
estimat3 # Por máxima verossimilhança.

## [1] 0.1723

anova(ajuste1, test='F') # Análise de deviance.

## Analysis of Deviance Table
## 
## Model: Gamma, link: identity
## 
## Response: tempo
## 
## Terms added sequentially (first to last)
## 
## 
##      Df Deviance Resid. Df Resid. Dev    F Pr(>F)   
## NULL                    49      12.97               
## turb  4      4.1        45       8.86 4.93 0.0022 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

O resultado do teste fornece evidência altamente significativa de diferença entre os tempos médios de vida das turbinas.

summary(ajuste1) 

## 
## Call:
## glm(formula = tempo ~ turb, family = Gamma(link = "identity"), 
##     data = PaulaTb2.1)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.0434  -0.3306  -0.0774   0.2169   1.1345  
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    10.693      1.543    6.93  1.3e-08 ***
## turbtipo II    -4.643      1.773   -2.62    0.012 *  
## turbtipo III   -2.057      1.983   -1.04    0.305    
## turbtipo IV    -0.895      2.093   -0.43    0.671    
## turbtipo V      4.013      2.624    1.53    0.133    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Gamma family taken to be 0.2082)
## 
##     Null deviance: 12.9654  on 49  degrees of freedom
## Residual deviance:  8.8616  on 45  degrees of freedom
## AIC: 285.9
## 
## Number of Fisher Scoring iterations: 3

A turbina II tem tempo médio de vida inferior à turbina I.

Vamos considerar a hipótese de que as turbinas podem ser divididas em três grupos, conforme os tempos de vida: Turbina II; Turbinas I, III e IV; Turbina V.

Vamos ajustar o mesmo MLG sob essa restrição (hipótese):

PaulaTb2.1$turb2 <- PaulaTb2.1$turb
levels(PaulaTb2.1$turb2) <- c('T134', 'T2', 'T134', 'T134', 'T5') 

Turb2 identifica as turbs I, III e IV da mesma forma.

ajuste2 <- glm(tempo ~ turb2, family = 'Gamma'(link = 'identity'), data = PaulaTb2.1)
anova(ajuste2, ajuste1, test='F') 

## Analysis of Deviance Table
## 
## Model 1: tempo ~ turb2
## Model 2: tempo ~ turb
##   Resid. Df Resid. Dev Df Deviance    F Pr(>F)
## 1        47       9.09                        
## 2        45       8.86  2    0.229 0.55   0.58

A diferença das deviances dos dois modelos não é significativa. Logo, podemos optar pelo modelo restrito, em que os tempos médios de vida das turbinas I, III e IV são iguais (p=0,5807).

summary(ajuste2)

## 
## Call:
## glm(formula = tempo ~ turb2, family = Gamma(link = "identity"), 
##     data = PaulaTb2.1)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -0.9763  -0.3307  -0.0515   0.2414   1.1474  
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    9.709      0.808   12.01  6.2e-16 ***
## turb2T2       -3.659      1.189   -3.08   0.0035 ** 
## turb2T5        4.997      2.269    2.20   0.0326 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Gamma family taken to be 0.2079)
## 
##     Null deviance: 12.9654  on 49  degrees of freedom
## Residual deviance:  9.0906  on 47  degrees of freedom
## AIC: 283.2
## 
## Number of Fisher Scoring iterations: 3

Assim, temos a turbina V como aquela com maior tempo médio de vida, seguida pelas turbs I, III e IV e a turb II tem menor tempo médio de vida.

Tentando a distribuição normal inversa.

ajuste3 <- glm(tempo ~ turb2, family = inverse.gaussian(link = 'identity'), data = PaulaTb2.1)
hnp(ajuste3)

## Inverse gaussian model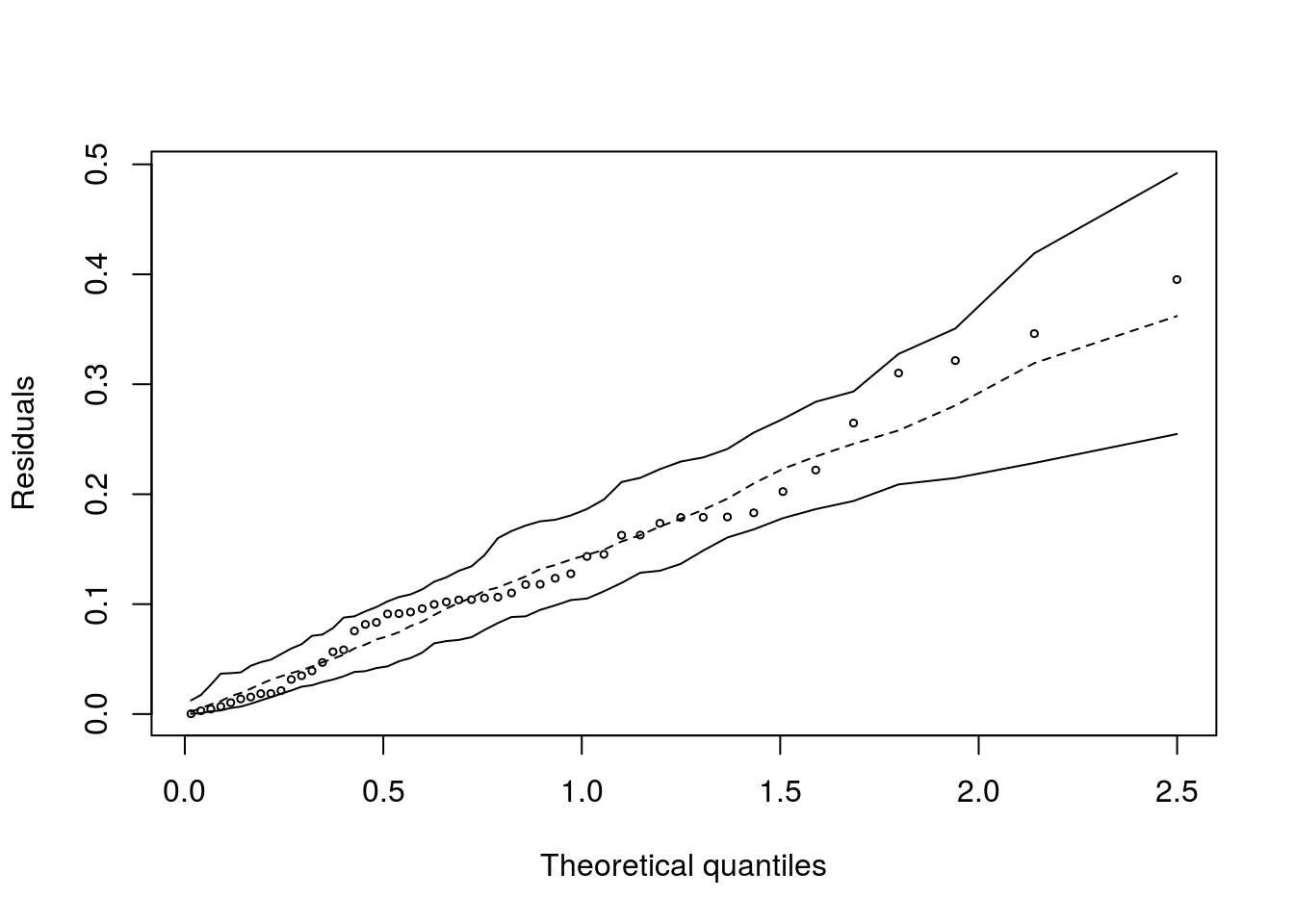

Vamos comparar as três distribuições usadas (normal, gama e normal inversa) com base nos AICs dos respectivos ajustes.

ajuste4 <- glm(tempo ~ turb2, family = gaussian(link = 'identity'), data = PaulaTb2.1)

AIC(ajuste2, ajuste3, ajuste4)

##         df   AIC
## ajuste2  4 283.2
## ajuste3  4 284.4
## ajuste4  4 295.5

Os dois modelos (gama e normal inverso) produziram AIC bastante próximos. Ainda assim, o modelo de regressão gama tem AIC ligeiramente menor e é preferível.