Besouros da farinha

Regressão para dados binários

require(ggplot2)
require(car)

Exemplo 2

Dados de mum experimento do tipo dose-resposta, referente à mortalidade de besouros sob três tratamentos (DDT, BHC e DDT+BHC), sob seis diferentes doses.

ldose <- log(rep(c(2, 2.64, 3.48, 4.59, 6.06, 8), 3)) ### log-dose

Trat <- rep(c('DDT', 'BHC', 'DDT+BHC'), each = 6) ### tratamento

Resposta <- c(3, 5, 19, 19, 24, 35, 2, 14, 20, 27, 41, 40, 28, 37, 46, 48, 48, 50)

Número de insetos mortos sob cada condição experimental.

n <- c(50, 49, 47, 50, 49, 50, 50, 49, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50)

Número de insetos submetidos a cada condição experimental.

dados <- data.frame(ldose,Trat,Resposta,n)

Análise descritiva

g0 <- ggplot(dados, aes(x = ldose, y = Resposta/n, color=Trat)) +
  geom_point(size = 4) + theme_bw(base_size = 18) + 
  labs(x = 'Dose(log)', y = 'Proporção de insetos mortos') +
  theme(legend.position="top")
g0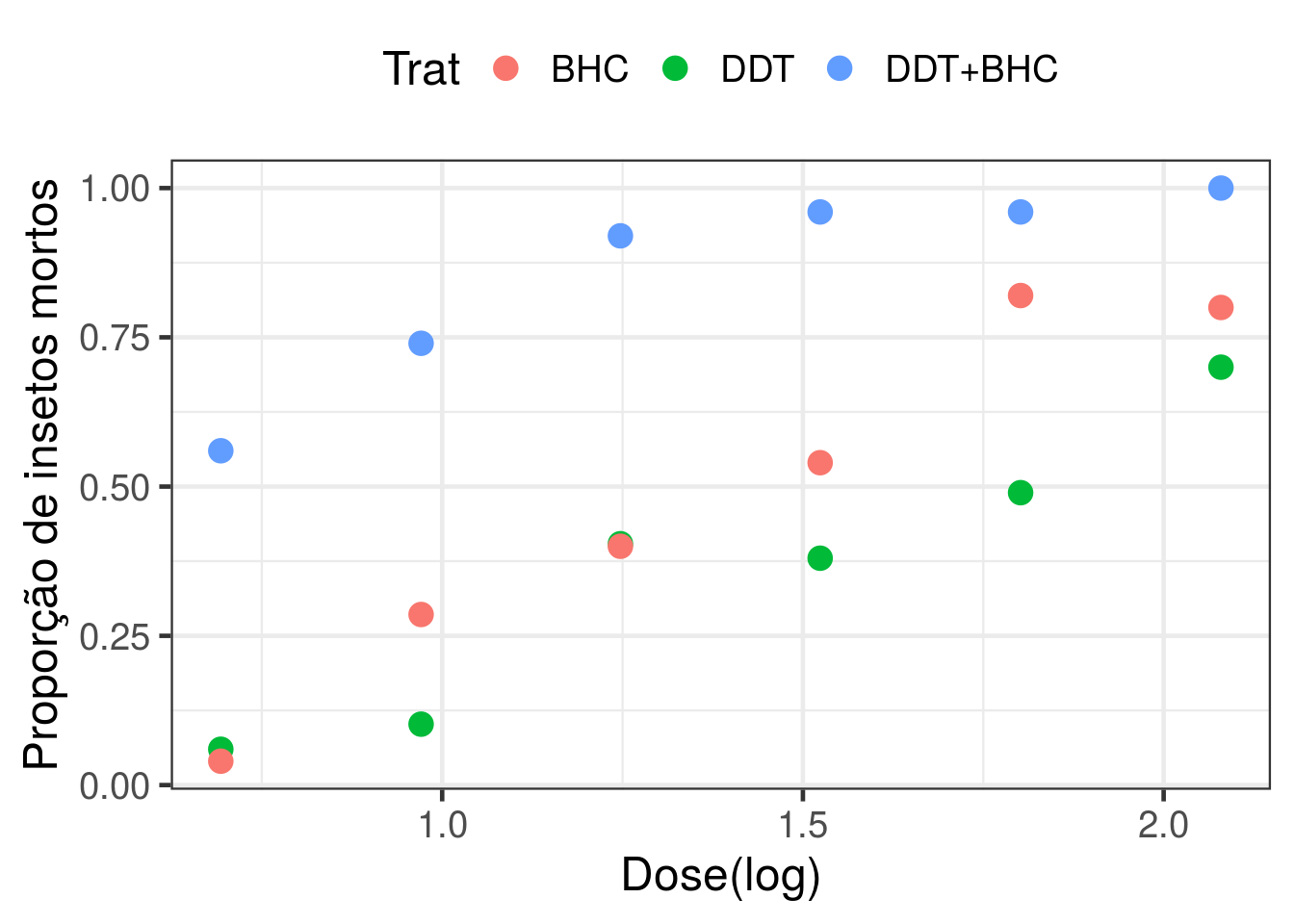

Parte 1

Vamos começar ajustando um modelo apenas para os insetos tratados com BHC

data_BCH <- subset(dados, Trat=='BHC')

g1 <- ggplot(data_BCH, aes(x = ldose, y = Resposta/n)) +
  geom_point(size = 4) + theme_bw(base_size = 18) + 
  labs(x = 'Dose(log)', y = 'Proporção de insetos mortos') +
  theme(legend.position="top")
g1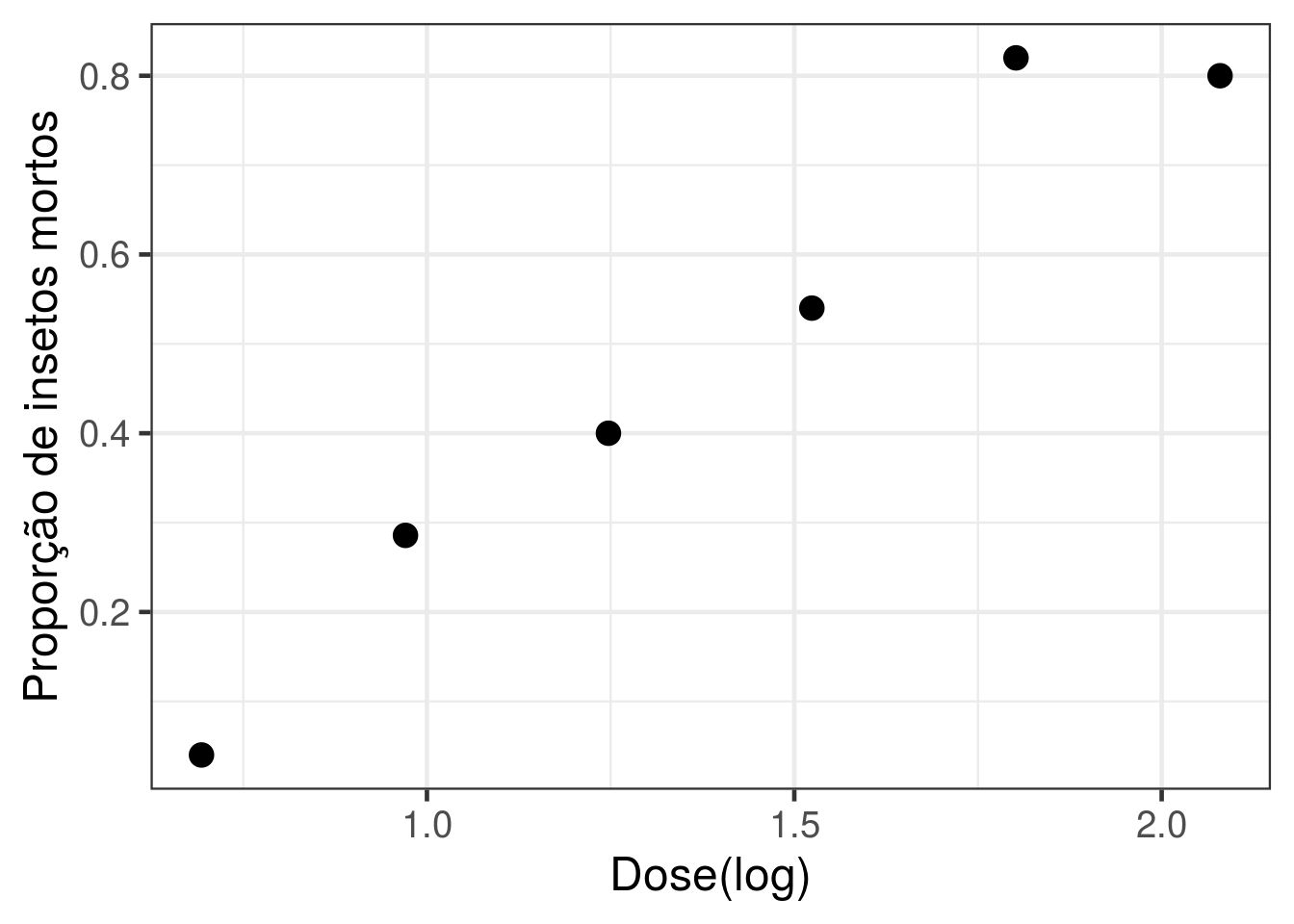

Modelo com função de ligação logito

ajuste1 <- glm(cbind(Resposta, n-Resposta) ~ ldose, family = binomial, 
               data = data_BCH)

A primeira forma de declarar a resposta quando temos um glm binomial com dados grupados é por umja matriz com duas colunas, cada uma delas com as contagens de um dos desfechos binários (insetos mortos e não mortos, no caso).

Forma alternativa:

ajuste1_2 <- glm(Resposta/n ~ ldose, family = binomial, data = data_BCH, weights = n)

Neste caso, declaramos a resposta como a fração de insetos mortos, e o número de insetos mortos é declarado em weights.

summary(ajuste1)

## 
## Call:
## glm(formula = cbind(Resposta, n - Resposta) ~ ldose, family = binomial, 
##     data = data_BCH)
## 
## Deviance Residuals: 
##       7        8        9       10       11       12  
## -1.8245   1.1416   0.3390  -0.4281   1.2679  -1.2728  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -4.0428     0.4972  -8.131 4.27e-16 ***
## ldose         2.8381     0.3392   8.367  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 105.1973  on 5  degrees of freedom
## Residual deviance:   8.1581  on 4  degrees of freedom
## AIC: 35.376
## 
## Number of Fisher Scoring iterations: 4

summary(ajuste1_2)

## 
## Call:
## glm(formula = Resposta/n ~ ldose, family = binomial, data = data_BCH, 
##     weights = n)
## 
## Deviance Residuals: 
##       7        8        9       10       11       12  
## -1.8245   1.1416   0.3390  -0.4281   1.2679  -1.2728  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -4.0428     0.4972  -8.131 4.27e-16 ***
## ldose         2.8381     0.3392   8.367  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 105.1973  on 5  degrees of freedom
## Residual deviance:   8.1581  on 4  degrees of freedom
## AIC: 35.376
## 
## Number of Fisher Scoring iterations: 4

Os modelos ajustados são rigorosamente os mesmos. Muda apenas a forma de declaração.

Exercício: Escreva a equação do modelo ajustado e calcule a estimativa da probabilidade de morte para insetos submetidos a uma dose de 7 unidades. Adicionalmente, interprete (se couber) os parâmetros do modelo.

Agora, vamos adicionar ao gráfico a curva referente ao modelo ajustado

grid_ldose <- seq(log(2), log(8), 0.01) ### grid de valores para a (log) dose.
preditos <- predict(ajuste1, newdata=data.frame(ldose = grid_ldose), type='response')

Probabilidades estimadas para as doses no grid que criamos

new.data <- data.frame(grid_ldose, preditos)

g2 <- g1 + geom_line(data = new.data, aes(x = grid_ldose, y = preditos),  
                     size = 1.2, color = 'black')
g2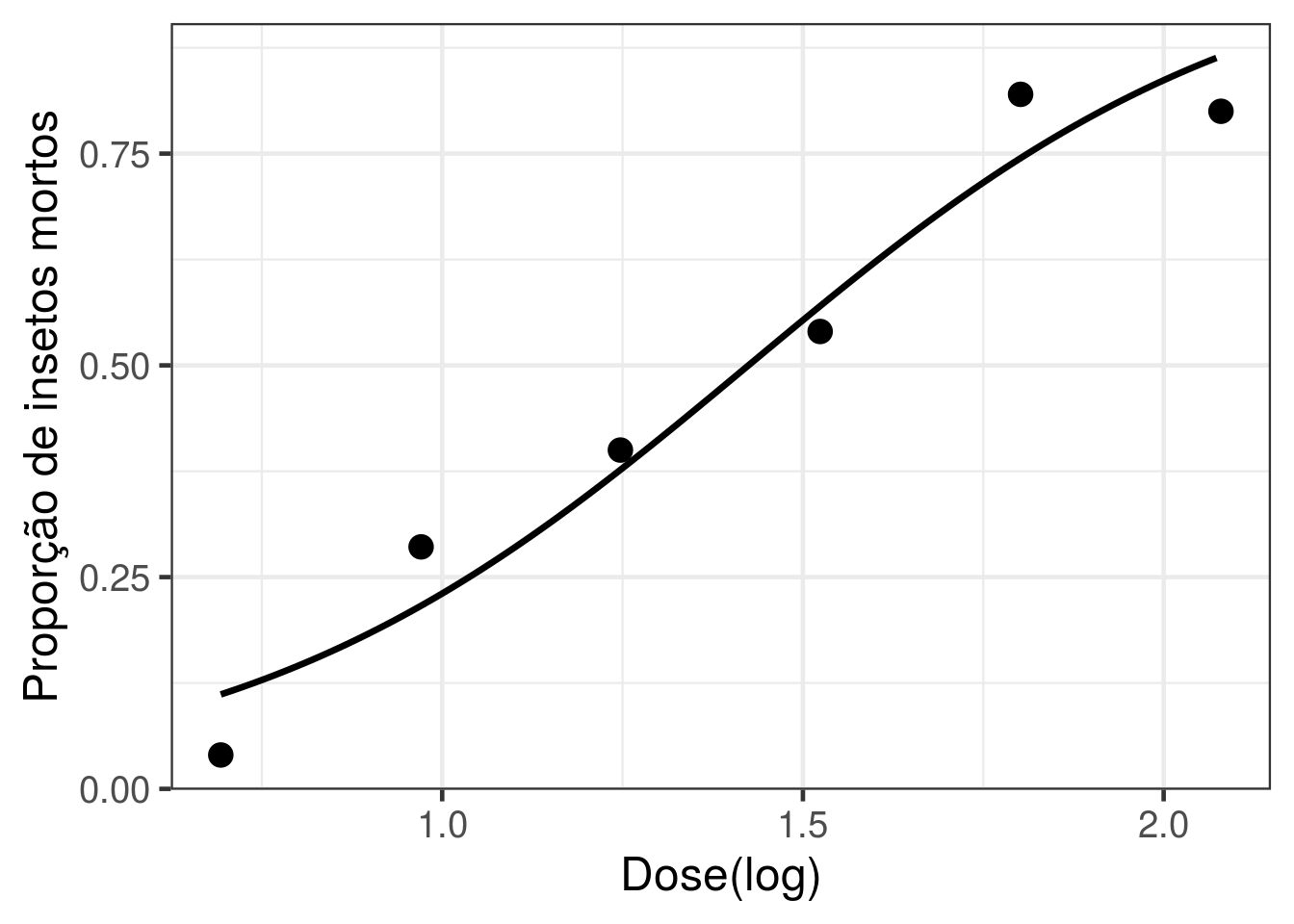

Modelo com função de ligação probito

ajuste2 <- glm(Resposta/n ~ ldose, family = binomial(link = 'probit'), 
               data = data_BCH, weights = n)
summary(ajuste2)

## 
## Call:
## glm(formula = Resposta/n ~ ldose, family = binomial(link = "probit"), 
##     data = data_BCH, weights = n)
## 
## Deviance Residuals: 
##       7        8        9       10       11       12  
## -1.6900   1.1213   0.3137  -0.3505   1.3744  -1.3053  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -2.4373     0.2764  -8.817   <2e-16 ***
## ldose         1.7062     0.1881   9.069   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 105.1973  on 5  degrees of freedom
## Residual deviance:   7.9272  on 4  degrees of freedom
## AIC: 35.145
## 
## Number of Fisher Scoring iterations: 4

Exercício: Escreva a equação do modelo ajustado e calcule a estimativa da probabilidade de morte para insetos submetidos a uma dose de 7 unidades.

Adicionando ao gráfico a curva referente ao odelo ajustado

preditos2 <- predict(ajuste2, newdata=data.frame(ldose = grid_ldose), type='response')
new.data2 <- data.frame(grid_ldose, preditos2)

g3 <- g2 + geom_line(data = new.data2, aes(x = grid_ldose, y = preditos2),  
                     size = 1.2, color = 'blue')
g3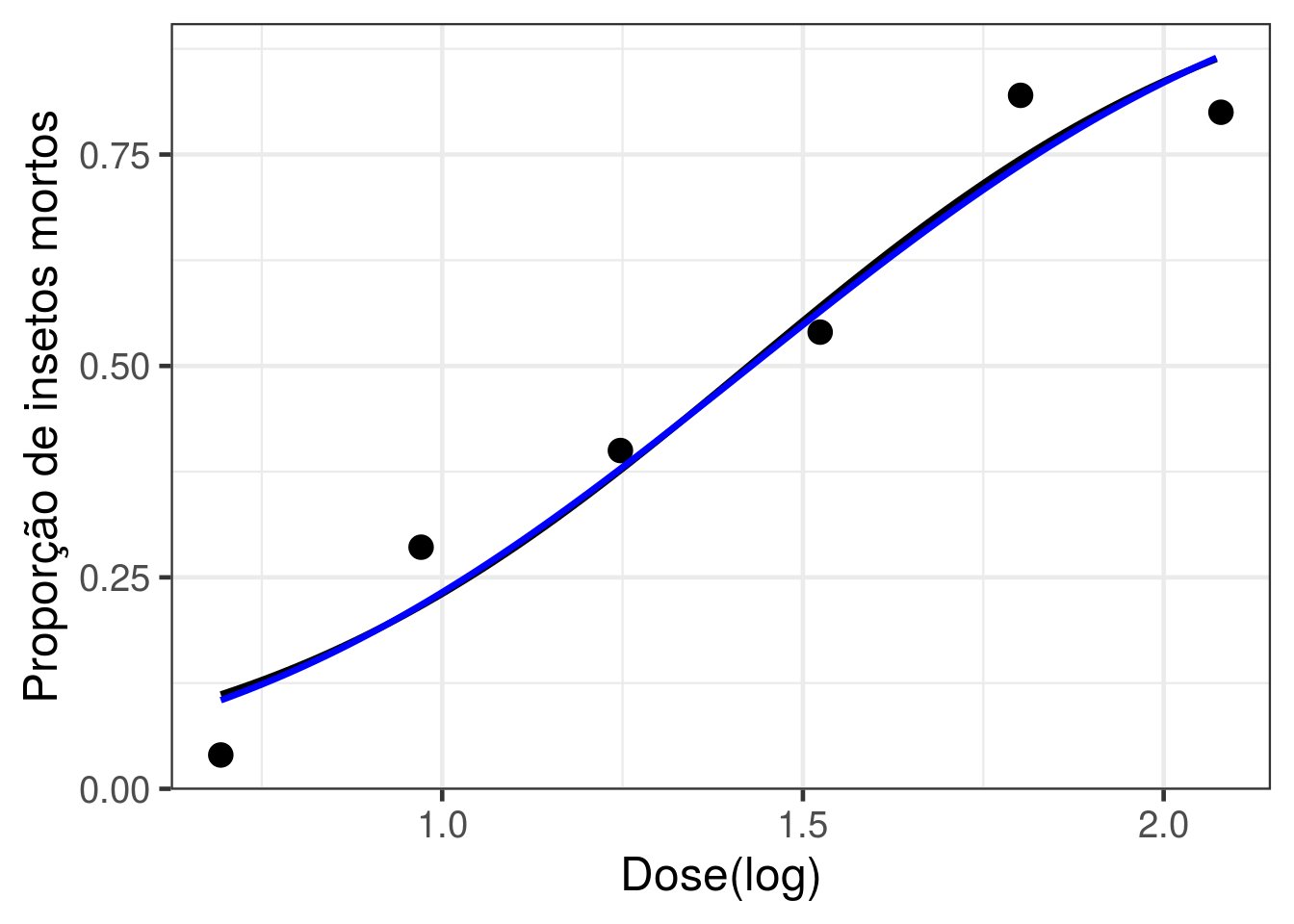

Modelo com função de ligação complemento log-log

ajuste3 <- glm(Resposta/n ~ ldose, family = binomial(link = 'cloglog'), 
               data = data_BCH, weights = n)
summary(ajuste3)

## 
## Call:
## glm(formula = Resposta/n ~ ldose, family = binomial(link = "cloglog"), 
##     data = data_BCH, weights = n)
## 
## Deviance Residuals: 
##       7        8        9       10       11       12  
## -2.4988   0.8083   0.5615   0.1727   1.7142  -1.5676  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -3.1170     0.3562  -8.751   <2e-16 ***
## ldose         1.8570     0.2166   8.575   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 105.197  on 5  degrees of freedom
## Residual deviance:  12.638  on 4  degrees of freedom
## AIC: 39.856
## 
## Number of Fisher Scoring iterations: 5

Exercício: Escreva a equação do modelo ajustado e calcule a estimativa da probabilidade de morte para insetos submetidos a uma dose de 7 unidades.

Adicionando ao gráfico a curva referente ao odelo ajustado

preditos3 <- predict(ajuste3, newdata = data.frame(ldose = grid_ldose), type='response')
new.data3 <- data.frame(grid_ldose, preditos3)

g4 <- g3 + geom_line(data = new.data3, aes(x = grid_ldose, y = preditos3),  
                     size = 1.2, color = 'green')
g4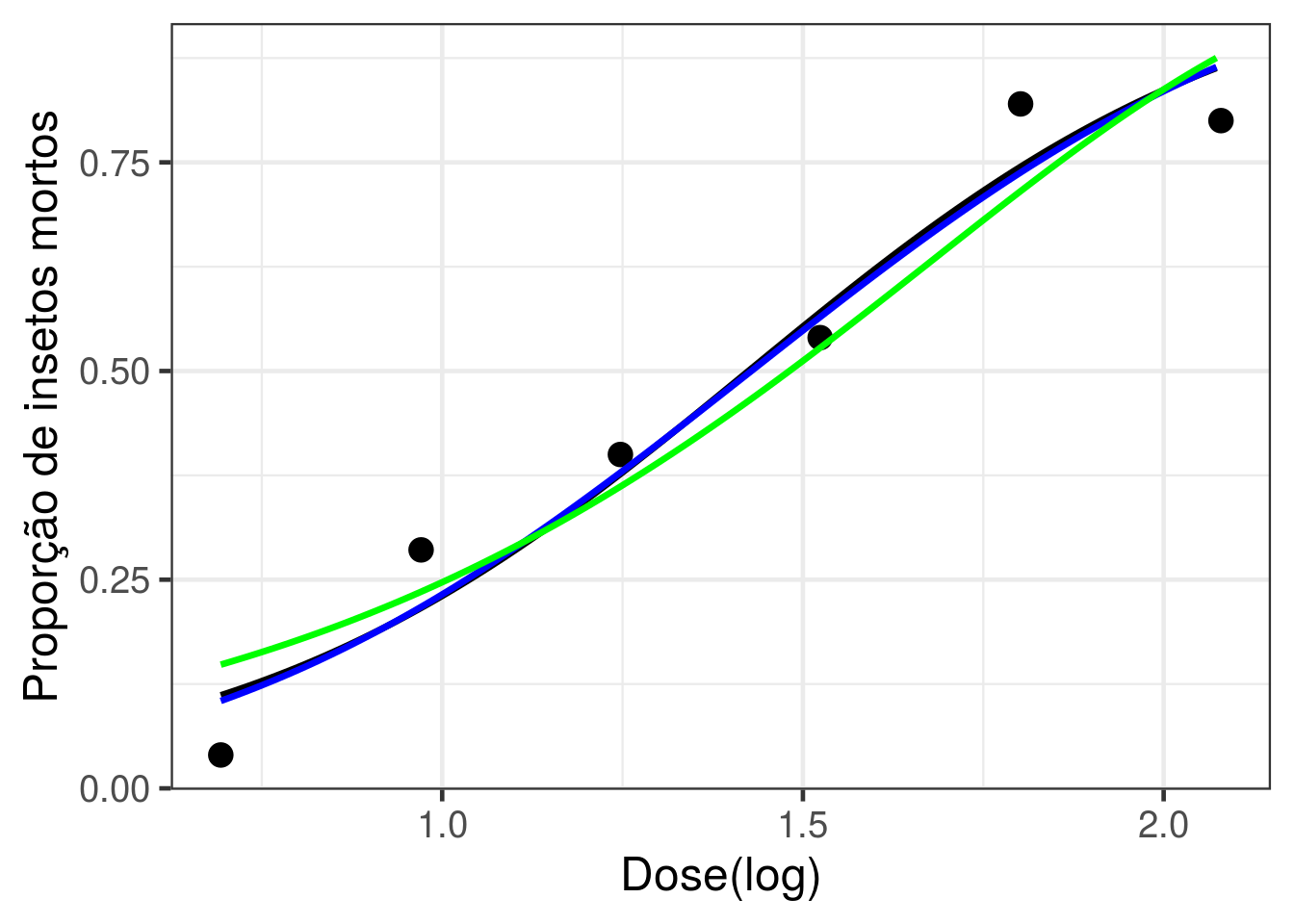

AIC

Vamos comparar os ajustes dos três modelos calculando os respectivos AICs.

AIC(ajuste1, ajuste2, ajuste3)

##         df      AIC
## ajuste1  2 35.37617
## ajuste2  2 35.14529
## ajuste3  2 39.85641

c(logLik(ajuste1), logLik(ajuste2), logLik(ajuste3))

## [1] -15.68809 -15.57264 -17.92820

Log-verossimilhanças maximizadas.

O modelo com ligação probito é ligeiramente superior ao com ligação logito. O modelo cloglog claramente tem pior ajuste que seus concorrentes.

E se ao invés de analisarmos os dados da forma como estão disponíveis (grupados) analisarmos na forma não grupada (ou seja, um inseto por linha)? Vamos construir uma nova base.

data_BCH2 <- data_BCH[rep(seq_len(nrow(data_BCH)), times=data_BCH$n),1:2]
respostas <- c(rbind(data_BCH$Resposta, data_BCH$n - data_BCH$Resposta)) 
data_BCH2$resp_bin <- rep(c(1,0,1,0,1,0,1,0,1,0,1,0), times = respostas)
head(data_BCH2, 20)

##          ldose Trat resp_bin
## 7    0.6931472  BHC        1
## 7.1  0.6931472  BHC        1
## 7.2  0.6931472  BHC        0
## 7.3  0.6931472  BHC        0
## 7.4  0.6931472  BHC        0
## 7.5  0.6931472  BHC        0
## 7.6  0.6931472  BHC        0
## 7.7  0.6931472  BHC        0
## 7.8  0.6931472  BHC        0
## 7.9  0.6931472  BHC        0
## 7.10 0.6931472  BHC        0
## 7.11 0.6931472  BHC        0
## 7.12 0.6931472  BHC        0
## 7.13 0.6931472  BHC        0
## 7.14 0.6931472  BHC        0
## 7.15 0.6931472  BHC        0
## 7.16 0.6931472  BHC        0
## 7.17 0.6931472  BHC        0
## 7.18 0.6931472  BHC        0
## 7.19 0.6931472  BHC        0

data_BCH2 é a base de dados desagregados. Agora, cada linha da base é o dado de um único besouro, e a resposta é 1, para os insetos mortos, e zero, para os vivos.

Vamos ajustar o modelo de regressão binomial com ligação logito à base de dados desagregada.

ajuste1_desag <- glm(resp_bin ~ ldose, family = binomial, data = data_BCH2) 
summary(ajuste1_desag)

## 
## Call:
## glm(formula = resp_bin ~ ldose, family = binomial, data = data_BCH2)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.0018  -0.6981  -0.4862   0.7678   2.0947  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -4.0428     0.4972  -8.131 4.27e-16 ***
## ldose         2.8381     0.3392   8.367  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 414.10  on 298  degrees of freedom
## Residual deviance: 317.06  on 297  degrees of freedom
## AIC: 321.06
## 
## Number of Fisher Scoring iterations: 4

E vamos comparar os ajustes dos modelos aplicados à base agregada e à base não agregada por meio das estimativas dos parâmetros e correspondentes erros padrões.

compareCoefs(ajuste1, ajuste1_desag)

## Calls:
## 1: glm(formula = cbind(Resposta, n - Resposta) ~ ldose, family = 
##   binomial, data = data_BCH)
## 2: glm(formula = resp_bin ~ ldose, family = binomial, data = data_BCH2)
## 
##             Model 1 Model 2
## (Intercept)  -4.043  -4.043
## SE            0.497   0.497
##                            
## ldose         2.838   2.838
## SE            0.339   0.339
##

Observe que o modelo ajustado às duas bases é idêntico. Então, usar a base de dados agregada ou não agregada não altera o resultado do ajuste.

logLik(ajuste1)

## 'log Lik.' -15.68809 (df=2)

logLik(ajuste1_desag)

## 'log Lik.' -158.529 (df=2)

As escalas das verossimilhanças, no entanto, são diferentes. Em particular, o teste da qualidade do ajuste, baseado na deviance residual, se aplica aos dados agregados (para n grande), mas não aos dados desagregados. Vamos avaliar a qualidade do ajuste.

pchisq(deviance(ajuste1), df = ajuste1$df.residual, lower.tail = FALSE)

## [1] 0.08595524

p-valor do teste da qualidade do ajuste. Ao nível de significância de 5% não temos evidência de que o modelo não se ajuste bem aos dados.

Exercício - Avaliar a qualidade dos ajustes com base nas deviances (teste ao nível de significância de 5%). Faça também qqplots com envelopes simulados.

Parte 2

Agora, vamos analisar os três tratamentos conjuntamente. Nesta
etapa, vamos usar apenas a função de ligação logito

Gráfico de dispersão.

h0 <- ggplot(dados, aes(x = ldose, y = Resposta/n, color=Trat)) +
     geom_point(size = 4) + theme_bw(base_size = 18) + 
     labs(x = 'Dose(log)', y = 'Proporção de insetos mortos') +
     theme(legend.position="top")
h0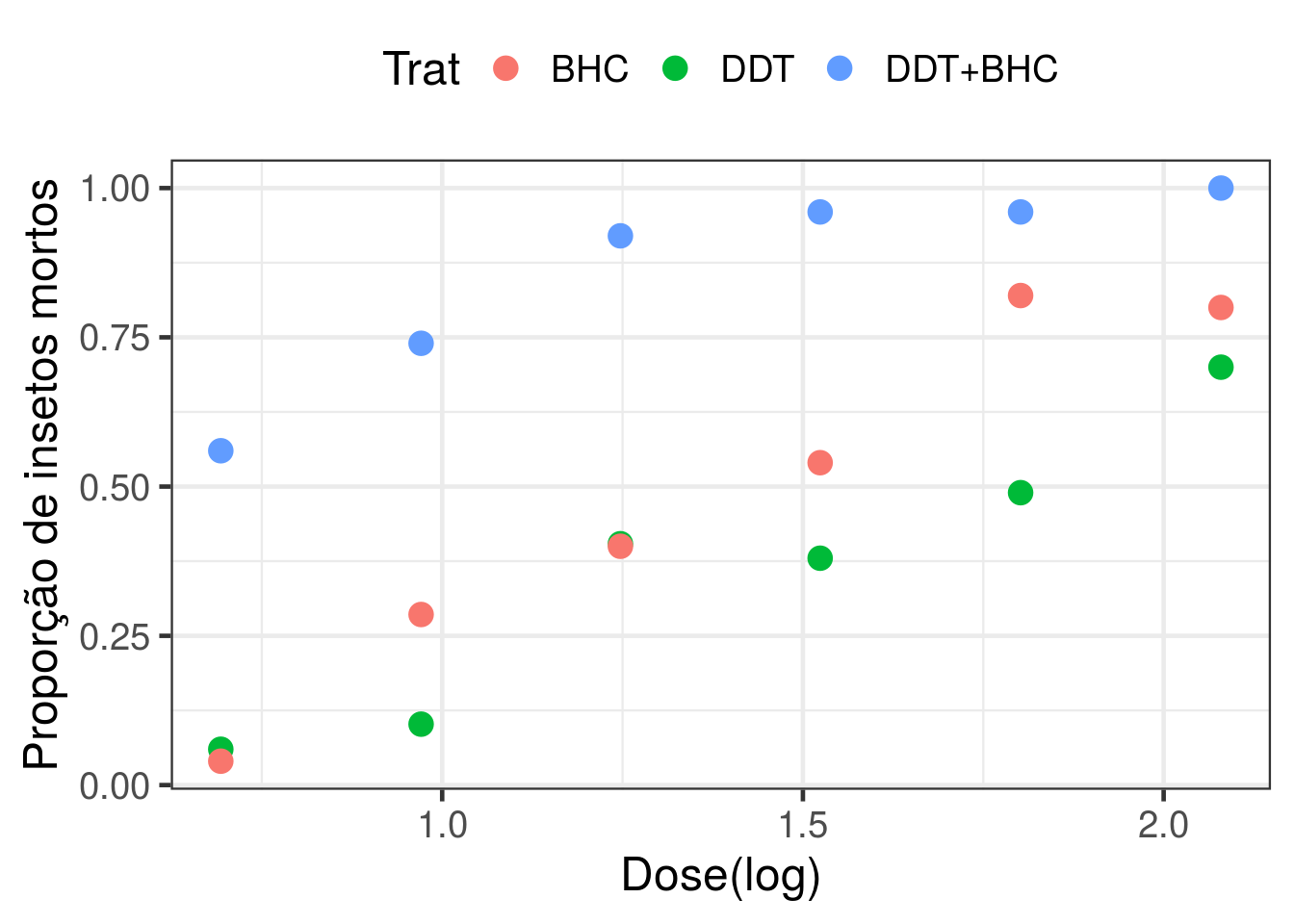

Conforme discutido em aula, vamos considerar três modelos, conforme descrito na sequência:

ajuste4 - Modelo de retas coincidentes - Sem considerar o efeito de tratamento. ajuste5 - Modelo de retas paralelas - Considerando o efeito de tratamento apenas no intercepto (modelo aditivo). ajuste6 - Modelo de retas concorrentes - Sem considerar o efeito de tratamento no intercepto e associado à dose (modelo multiplicativo - com efeito de interação)..

Modelo de retas coincidentes

ajuste4 <- glm(cbind(Resposta,n-Resposta) ~ ldose, family = binomial, data = dados)

Este é o modelo mais simples, em que ajustamos uma única reta (na escala do preditor, curva na escala da resposta) para os três tratamentos.

summary(ajuste4)

## 
## Call:
## glm(formula = cbind(Resposta, n - Resposta) ~ ldose, family = binomial, 
##     data = dados)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -4.336  -3.381  -1.384   4.024   6.301  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -2.4653     0.2386  -10.33   <2e-16 ***
## ldose         2.0106     0.1703   11.81   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 413.65  on 17  degrees of freedom
## Residual deviance: 246.83  on 16  degrees of freedom
## AIC: 314.3
## 
## Number of Fisher Scoring iterations: 5

Adicionando o modelo ajustado ao gráfico.

preditos4 <- predict(ajuste4, newdata=data.frame(ldose = grid_ldose), type='response')
new.data4 <- data.frame(grid_ldose, preditos4)

h1 <- h0 + geom_line(data = new.data4, aes(x = grid_ldose, y = preditos4),  
                     size = 1.2, color = 'black')
h1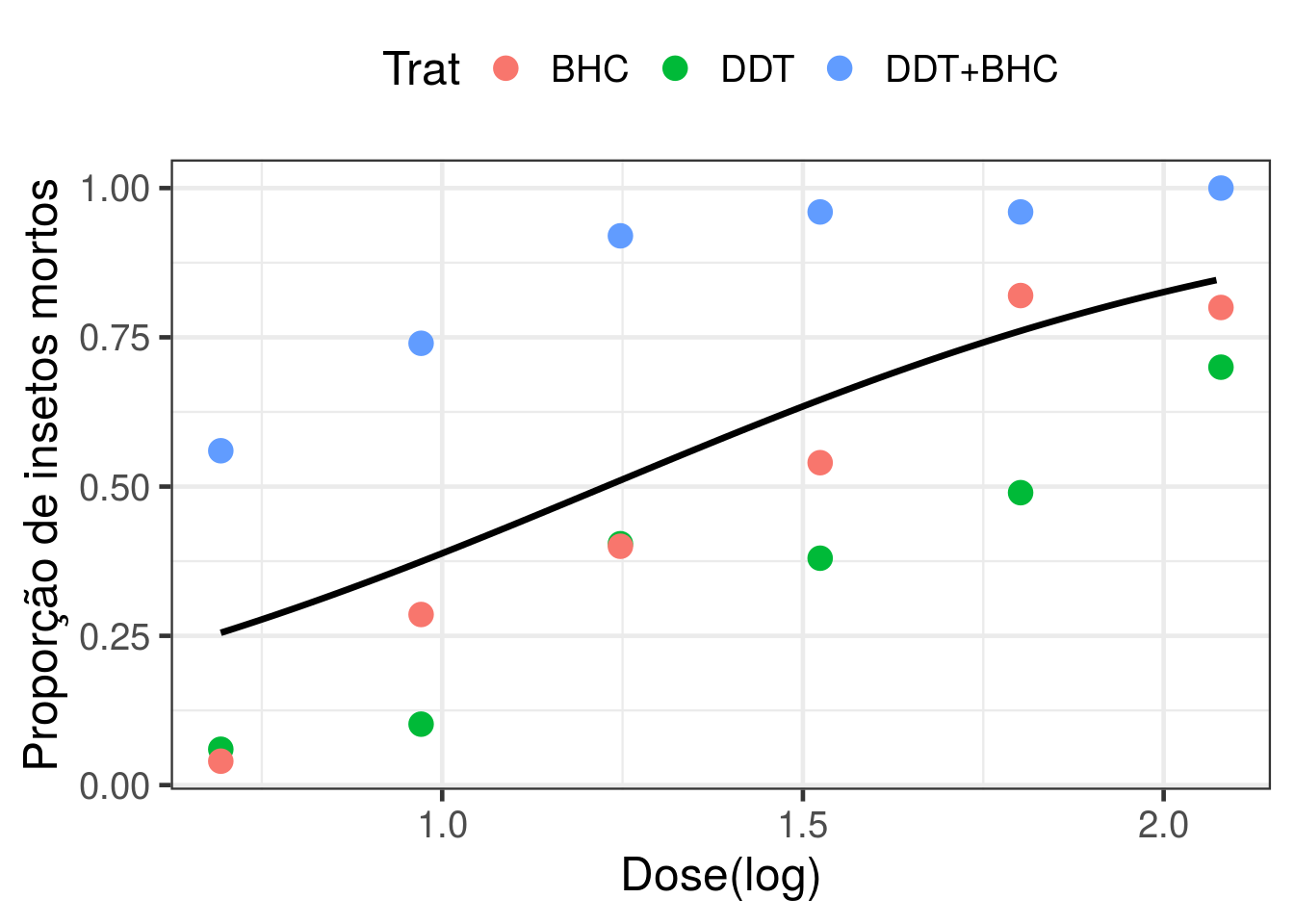

Modelo de retas paralelas

ajuste5 <- glm(cbind(Resposta,n-Resposta) ~ ldose + Trat, family = binomial, data = dados)

Este é o modelo intermediário (aditivo), em que ajustamos retas paralelas (na escala do preditor) para os três tratamentos.

summary(ajuste5)

## 
## Call:
## glm(formula = cbind(Resposta, n - Resposta) ~ ldose + Trat, family = binomial, 
##     data = dados)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.0270  -0.6160  -0.2422   0.9016   2.6120  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -3.8425     0.3327 -11.550  < 2e-16 ***
## ldose         2.6958     0.2157  12.498  < 2e-16 ***
## TratDDT      -0.7128     0.1981  -3.598  0.00032 ***
## TratDDT+BHC   2.4177     0.2381  10.154  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 413.648  on 17  degrees of freedom
## Residual deviance:  21.282  on 14  degrees of freedom
## AIC: 92.753
## 
## Number of Fisher Scoring iterations: 4

Agora, para predição precisamos de um grid de valores para cada inseticida. Vamos usar a função expand.grid para isso.

trat <- levels(dados$Trat)
grid_trat <- expand.grid(grid_ldose, trat)
names(grid_trat) <- c("grid_ldose", "trat")
preditos5 <- predict(ajuste5, newdata = data.frame(ldose = grid_trat[,1], Trat = grid_trat[,2]), 
                     type='response')
new.data5 <- data.frame(grid_trat, preditos5)

h0 + geom_line(data = subset(new.data5, trat == 'BHC'), aes(x = grid_ldose, y = preditos5),  
               size = 1.2, color = 'red') +
     geom_line(data = subset(new.data5, trat == 'DDT'), aes(x = grid_ldose, y = preditos5),  
               size = 1.2, color = 'green') +
     geom_line(data = subset(new.data5, trat == 'DDT+BHC'), aes(x = grid_ldose, y = preditos5),  
               size = 1.2, color = 'blue')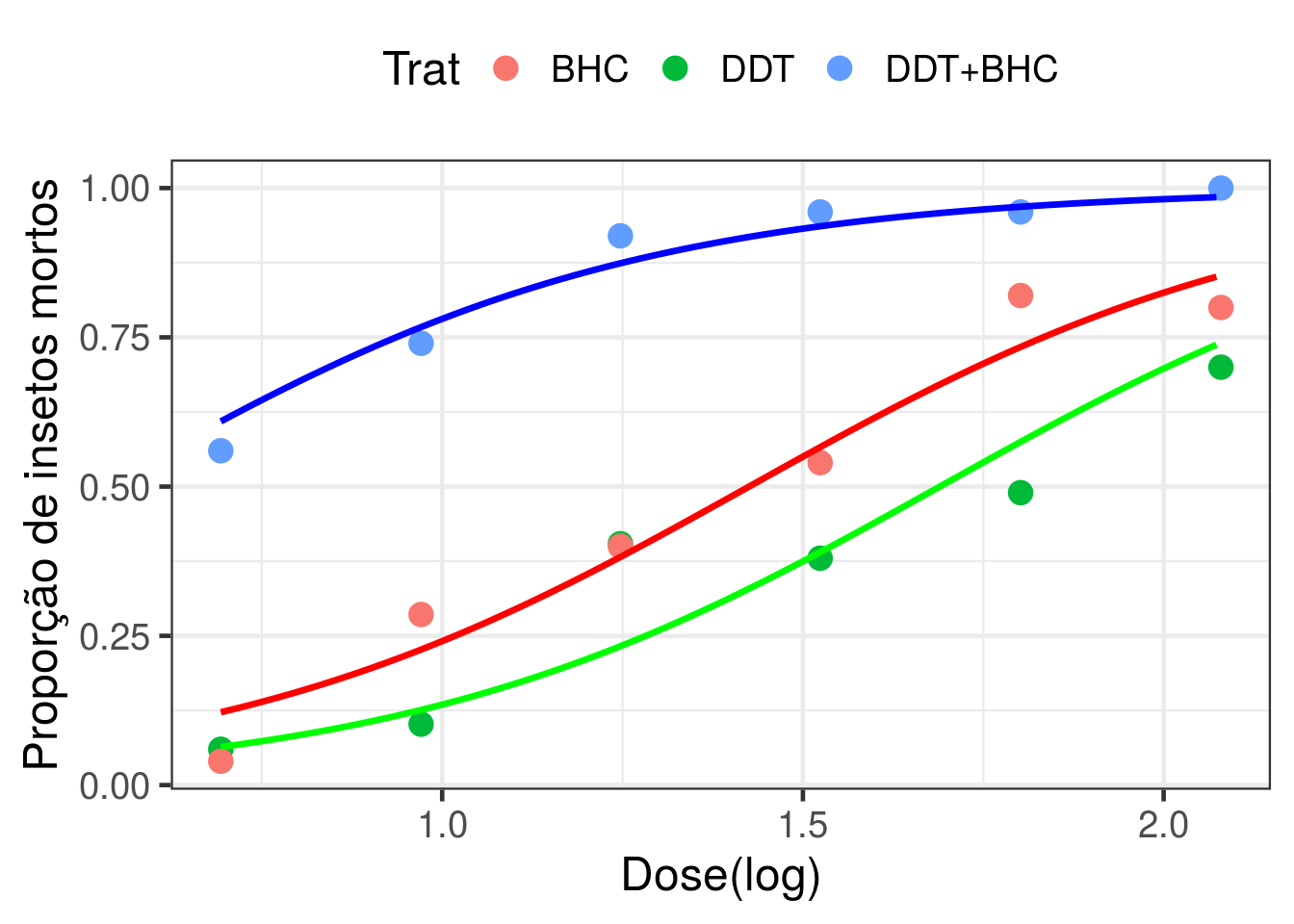

Adicionando as curvas de mortalidade vs dose para cada inseticida.

Modelo de retas concorrentes

ajuste6 <- glm(cbind(Resposta, n-Resposta) ~ ldose * Trat, family = binomial, data = dados)

Este é o modelo mais completo (multiplicativo - com interação), em que ajustamos retas concorrentes (na escala do preditor) para os três tratamentos.

summary(ajuste6)

## 
## Call:
## glm(formula = cbind(Resposta, n - Resposta) ~ ldose * Trat, family = binomial, 
##     data = dados)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -1.82453  -0.78870  -0.05548   0.59419   2.24095  
## 
## Coefficients:
##                   Estimate Std. Error z value Pr(>|z|)    
## (Intercept)        -4.0428     0.4972  -8.131 4.27e-16 ***
## ldose               2.8381     0.3392   8.367  < 2e-16 ***
## TratDDT             0.1278     0.7118   0.180   0.8575    
## TratDDT+BHC         1.9221     0.7722   2.489   0.0128 *  
## ldose:TratDDT      -0.5602     0.4680  -1.197   0.2313    
## ldose:TratDDT+BHC   0.5503     0.6662   0.826   0.4088    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 413.65  on 17  degrees of freedom
## Residual deviance:  17.89  on 12  degrees of freedom
## AIC: 93.361
## 
## Number of Fisher Scoring iterations: 4

preditos6 <- predict(ajuste6, newdata = data.frame(ldose = grid_trat[,1], Trat = grid_trat[,2]), type='response')
new.data6 <- data.frame(grid_trat, preditos6)

h0 + geom_line(data = subset(new.data6, trat == 'BHC'), aes(x = grid_ldose, y = preditos6),  
               size = 1.2, color = 'red') +
     geom_line(data = subset(new.data6, trat == 'DDT'), aes(x = grid_ldose, y = preditos6),  
               size = 1.2, color = 'green') +
     geom_line(data = subset(new.data6, trat == 'DDT+BHC'), aes(x = grid_ldose, y = preditos6),  
               size = 1.2, color = 'blue')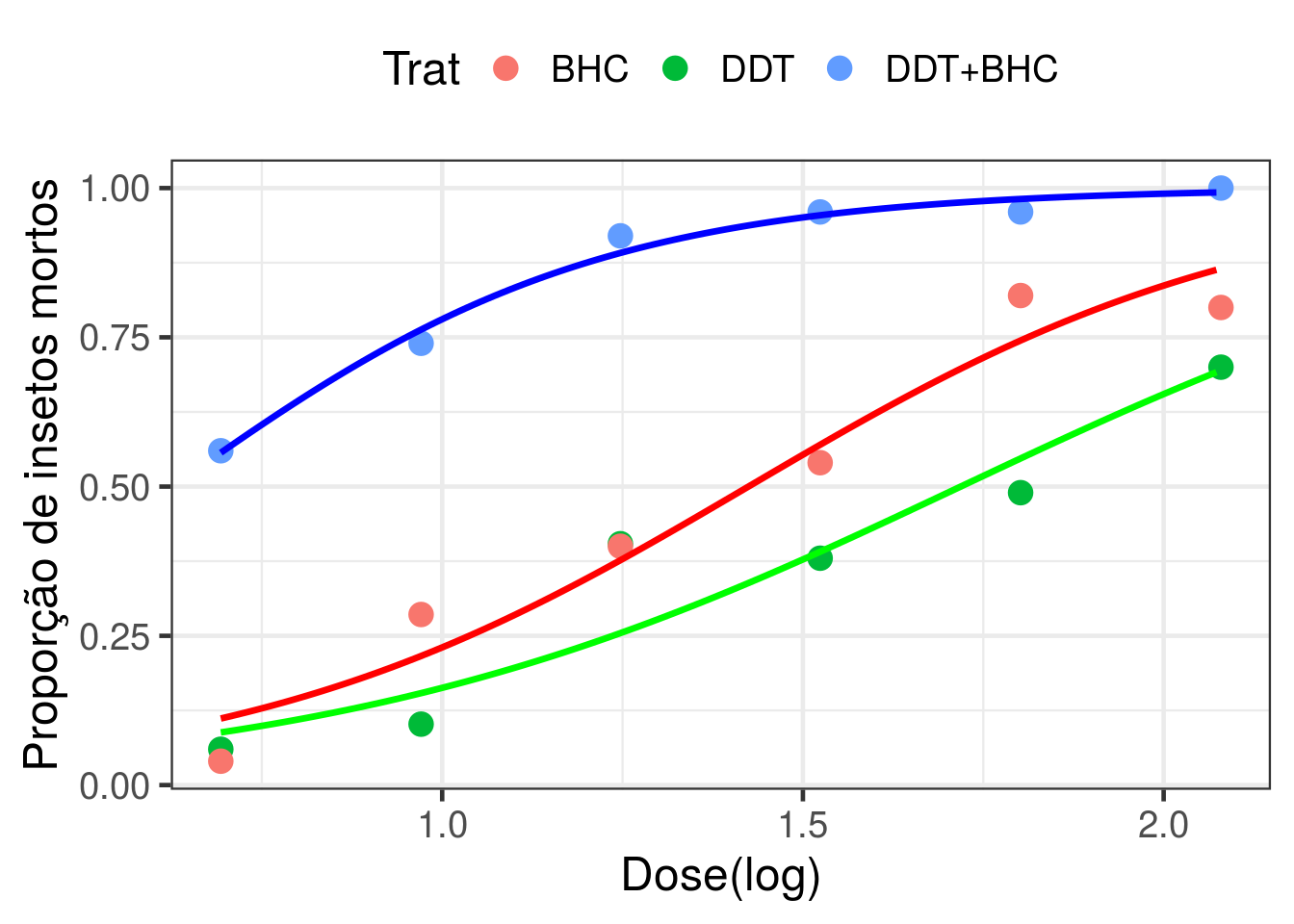

Comparação dos ajustes dos três modelos

Pelo fato dos três modelos serem encaixados, vamos compará-los usando o TRV.

anova(ajuste4, ajuste5, ajuste6, test = 'Chisq')

## Analysis of Deviance Table
## 
## Model 1: cbind(Resposta, n - Resposta) ~ ldose
## Model 2: cbind(Resposta, n - Resposta) ~ ldose + Trat
## Model 3: cbind(Resposta, n - Resposta) ~ ldose * Trat
##   Resid. Df Resid. Dev Df Deviance Pr(>Chi)    
## 1        16    246.832                         
## 2        14     21.282  2  225.550   <2e-16 ***
## 3        12     17.890  2    3.392   0.1834    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Repare, olhando para as duas primeiras linhas, que os modelos de retas coincidentes e retas paralelas produzem desvios significativamente diferentes. Nesse caso, dentre os dois modelos, optamos pelo não restrito (retas paralelas). No entanto, ao observar as duas últimas linhas, verificamos que os dois ajustes produzem desvios que não apresentam diferença significativa. Nesse caso, podemos optar pelo modelo restrito (retas paralelas). Pela análise dos desvios, baseado nos TRVs, o modelo de retas paralelas (efeito de tratamento no intercepto) é preferível.

AIC(ajuste4,ajuste5,ajuste6)

##         df       AIC
## ajuste4  2 314.30301
## ajuste5  4  92.75286
## ajuste6  6  93.36065

Repare que também através dos AICs tem-se indicativo de melhor ajuste para o modelo de retas paralelas.

Observando os resultados do summary, verifica-se que o modelo de retas paralelas tem deviance 21,282, associado a 14 graus de liberdade. Vamos testar a qualidade do ajuste.

pchisq(21.282, 14, lower.tail = F)

## [1] 0.09462121

Ao nível de significância de 5% não se tem evidência significativa de falta de ajuste.

Exercício - Para o modelo escolhido:

1- Escrever o modelo ajustado na escala do preditor, da chance e da probabilidade de resposta; 2- Interpretar as estimativas dos parâmetros do modelo; 3- Obter ICs 95% para os parâmetros do modelo; 4- Estimar a probabilidade de morte para doses de 3 e 7 unidades para cada tratamento. 5- Obter ICs 95% para as probabilidades mencionadas no item anterior; 6- Estimar, para cada tratamento, as doses letais 50% e 90%; 7- Fazer uma análise de diagnóstico, baseada na avaliação dos resíduos e de medidas de influência.